Hegyesszögű háromszög

Az ABC háromszögben AMN = 150°, mivel az AMB és ANC szögei egyenlőek, és egyenlő szárú háromszögben a két szög összege 180°.
Mivel a háromszög szögei összege 180°, ezért az ABC szöge az AMB és ANC szögeinek összege: 180° - 150° = 30°.
Az AMB és ANC szögei pedig 90°, mivel hegyesszögű háromszögben a szárak egyenlő szögűek.
Az ABC háromszög szögei: A = 90°, B = 30°, C = 60°.

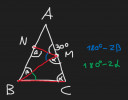
Csatolt képen a szöveg szerinti háromszög. A piros szakaszok mind egyenlők. Továbbá vezessük be a képen látható módon az ` alpha, beta ` valamint az ezekkel kifejezhető zöld és kék szögeket. Így két egyenletet tudunk felírni:

A ` B ` csúcsnál lévő két szög összege megegyezik ` alpha `-al, mivel az ` ABC ` egyenlőszárú háromszögben ` BC ` az alap, és az alapokon fekvő szögek egyenlők. Így:
` beta+180^{\circ}-2alpha = alpha Rightarrow beta+180^{\circ} = 3alpha `

A másik egyenletet úgy kapjuk, hogy az ` M ` csúcsnál lévő három szög együtt kiadja a 180°-ot, hiszen egy egyenesen fekszenek és a megfelelő szögszárak közösek. A 180°-hoz még 180°-30° = 150° hiányzik, így a másik egyenlet:
` alpha+180^{\circ}-2beta = 150^{\circ} Rightarrow alpha+30^{\circ} = 2beta `

Tehát a következő egyenletrendszert kell megoldanunk:

1) ` beta+180^{\circ} = 3alpha `

2) ` alpha+30^{\circ} = 2beta `

Az első egyenletből ` beta `-t kifejezve, és beírva a második egyenletbe:

` alpha+30^{\circ} = 6alpha-360^{\circ} \text{/}-alpha, +360^{\circ}`

` 5alpha = 390^{\circ} \text{/}:5 `

` alpha = 78^{\circ} `

Tehát a ` C ` csúcsnál lévő szög, és így a ` B ` csúcsnál lévő szög is: ` 78^{\circ} `

Az ` A ` csúcsnál lévő szög pedig így: ` 180^{\circ}-2*78^{\circ} = 24^{\circ} `