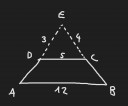
1) A trapéz szárainak hosszát a trapéz alapjának hosszának összege és az kiegészítő háromszög oldalainak hossza adja. Az alapok összege: 5 cm + 12 cm = 17 cm. Az oldalak hossza: 3 cm + 4 cm = 7 cm. A trapéz szárainak hossza: 17 cm + 7 cm = 24 cm.

2) Ha a háromszög kerülete 25,65 cm, és az oldalak hosszai 4 cm, 6 cm és 9 cm, akkor a hozzá hasonló háromszög oldalai mekkoraak?
A háromszög kerülete: 4 cm + 6 cm + 9 cm = 19 cm.
A hozzá hasonló háromszög oldalai: (25,65cm/19cm) * (4cm, 6cm, 9cm) = (1.35, 1.53, 1.8) cm

3) Egy háromszög oldalai 4 cm, 5 cm és 7 cm. Mekkorák a hozzá hasonló háromszög oldalai, ha a leghosszabb és legrövidebb oldalának különbsége 6 cm?
The similar triangle sides can be calculated by multiplying the ratio of the difference between the longest and shortest side of the given triangle and the similar triangle. The ratio is 6cm/2cm = 3. The similar triangle sides: 3*(4cm, 5cm, 7cm) = (12cm, 15cm, 21cm)

4) A világítótorony magasságát a világítótorony árnyékának és egy bot árnyékának arányából számíthatjuk ki. A bot magassága 220 cm. Az arány: 22 m / 1,6 m = 13,75. A világítótorony magassága: 13,75 * 220 cm = 3030 cm = 30,3 m.

1.) Első képen a trapéz. A rajzolt ábrán szimmetrikusnak tűnik a trapéz, de nyilván nem lesz az. Az ABE nagy háromszög hasonló a DCE kis háromszöghöz, mert az E csúcsnál kévő szög közös, a D és C csúcsoknál lévő szögek pedig rendre egyállású szögek az A és B csúcsnál lévő szögekkel, így páronként egyenlők. A hasonlóság miatt a megfelelő oldalpárok arányai megegyeznek a háromszögben. Így:
` 5/12=3/(AD+3) Rightarrow 5AD+15=36 Rightarrow AD = 4.2` cm

` 5/12=4/(CB+4) Rightarrow 5CB+20 = 48 Rightarrow 5.6 ` cm

2.) Az eredeti háromszög kerülete: ` 4+6+9=19 ` cm. A kerületeket összehasonlítva a hasonlóság aránya a két háromszög között: ` \lambda = 25.65/19 = 1.35 `. Ezzel a számmal szorozva az eredeti háromszög oldalainak hosszát megkapjuk a másik háromszög oldalait:
` a=4*1.35=5.4 \quad b=6*1.35=8.1 \quad c=9*1.35=12.15 `.

3.) Az eredeti háromszögben a leghosszab és legrövidebb oldal különbsége: 7-4=3. A hasonló háromszögben ez a különbség ennek a duplája, tehát a hasonlóság aránya ` lambda = 2 ` így a hasonló háromszögben minden oldal az eredeti kétszerese, tehát az oldalak, 8,10,14 cm.

4.) Jelöljük ` x `-el a világítótorony magasságát. A világítótorony és a bot is az árnyékaikkal együtt megfeleltethetőek egy-egy derékszögű háromszögnek. Ez nyilván hasonlóak, hiszen ugyanakkor ugyanott a nap ugyanakkora szögben süt rájuk, így az árnyékok szögei is megegyeznek. A hasonlóság miatt a megfelelő oldalpárok arányai megegyeznek:
` x/22 = 2.2/1.6 Rightarrow x=30.25` m.