Adva van egy háromszög három csúcsa a koordináta rendszerben: ` (x_1,y_1), (x_2,y_2), (x_3,y_3) `.
Ekkor a területe számolható a ` T = 1/2* |x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)| ` képlettel.
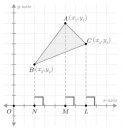
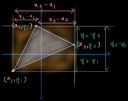
Ezt a képletet kétféleképpen nyerhetjük. Az 1. képen látható módon levetítjük a háromszög csúcsait az x tengelyre. Ekkor belátható, hogy a háromszög területe egyenlő: ABNM trapéz + ACLM trapéz - NBCL trapéz. Az oldalhozzok a megfelelő koordináták különbségeiből nyerhetőek, és egy kis algebrázás után eljutunk a felírt formátumhoz. A másik mód (2.kép), hogy a háromszöget egy téglalapba foglaljuk, és a téglalap területéből levonjuk a 3 kisebb derékszögű háromszög területét. Az oldalhosszok most is a megfelelő koordináták különbségeiből jönnek és most is szükség van némi algebrázásra. Mindkét esetben mivel az egyes pontok sorrendjét/szerepét önkényesen választjuk, egyes különbségek lehetnek negatívak is (emiatt a zárójelekben lévő különbségek sorrendje nem számít), erről viszont gondoskodik az abszolút érték, a távolságok pedig előjeltől függetlenül nyilván ugyanazok.

Az abszcissza és az ordináta egy másik elnevezése az x és y koordinátáknak. A harmadik pont első koordinátáját nem ismerjük, jelöljük ` x `-el, ezt keressük a feladat feltételének megfelelően.

Tehát a három pontunk ` A(0;5)\quad B(4;0)\quad C(x;7) `

Felhasználva a korábban bemutatott képletet:
` 1/2*|0(0-7)+4(7-5)+x(5-0)| = 9 `

` 1/2*|5x+8| = 9 \text{/}*2`

` |5x+8| = 18 `

Abszolútértékes egyenletet kell megoldanunk, így esetszétválasztást csinálunk: ` 5x+8 = 0 \Leftrightarrow x=-8/5 `
Ha ` x ` ettől kevesebb, akkor az abszolútérték belseje negatív, ha ettől több vagy egyenlő, akkor nemnegatív. Így a következő eseteket kell vizsgálni:
1) ` x < -8/5 `

` -5x-8 = 18 \text{/}+8 `

` -5x = 26\text{/}:(-5) `

` x = -26/5 < -8/5 \quad ` Ez jó megoldás.

2) ` x \geq -8/5 `

` 5x+8 = 18 \text{/}-8`

` 5x = 10 \text{/}:5`

` x = 2 \geq -8/5 \quad ` Ez is jó megoldás.

Tehát ` x\in {-26/5;2} `