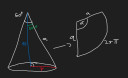
Csatolt képen az ábra. A nyílásszög a kúp csúcsánál lévő szöget jelenti. A kúp belsejébe rajzolható egy a képen látható derékszögű háromszög. Ennek a rövidebbik befogója éppen az alapkör sugara, átfogója a kúp alkotója. Előbbi számolható trigonometriával:

` \text{tg} 30° = r/10 \Rightarrow \sqrt{3}/3 = r/10 \text{/}*10 \Rightarrow r=(10\sqrt{3})/3 `
Az alkotó is számolható trigonometriával, de lehet Pitagorasz tétellel is:
` a = \sqrt{10^2+((10\sqrt{3})/3)^2} = \sqrt{400/3} = 20/\sqrt{3}`

A kiterített palást két egyenes oldala a kúp alkotója, az ívhossza pedig az alapkör kerülete. Az ívhossz így: ` 2*(10\sqrt{3})/3\pi = (20\sqrt{3})/3\pi `.
A palást megfelel egy körcikknek. Körcikkben igaz, hogy középponti szög (radiánban)·sugár = ívhossz:
` \overset(frown)\alpha\cdot 20/\sqrt{3} = (20\sqrt{3})/3\pi \Rightarrow \overset(frown)\alpha=\pi = 180^{\circ}`

Körcikk területe (egyik lehetséges): ívhossz*sugár/2. De most mivel 180° a középponti szög, ez éppen egy teljes kör fele lesz, így: ` \frac{(20/\sqrt{3})^2\pi}{2} = 200/3\pi`

Kúp felszíne: alapkör+palást területe. ` A= ((10\sqrt{3})/3)^2\pi + 200/3\pi = 100\pi ` cm2
Kúp térfogata: `V = (r^2\pi\cdot m)/3 = (100/3\pi\cdot 10)/3 = 500/3\pi ` cm3