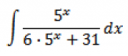Keresés


Toplista

Toplista
  • betöltés...

Magántanár kereső

Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!

Integrálás

432
Elakadtam :(

Ennél melyik módszert kell alkalmazni? :(

A legtöbb feladat megy, de van 1-1, amelyikbe belezavarodok. :(
Pedig elvileg megtanultam a szabályokat... :/
Feladat kép
Jelenleg 1 felhasználó nézi ezt a kérdést.
analízis, határozatlan, integrálás
0
Felsőoktatás / Matematika

Válaszok

1
Helyettesítéses integrálás: legyen `u=6*5^x+31`, ekkor `du=6ln5*5^xdx`, vagyis `dx=1/(6ln5*5^x)du`. Helyettesítsük be az integrálba:

`int ((5^x)/u 1/(6ln5*5^x)du)=1/(6ln5) int 1/u du=1/(6ln5)(lnu+C)=ln(6*5^x+31)/(6ln5)+D`
1