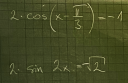Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Szimpla 10.- ik es Trigonomiai matek
 brinyiczki
kérdése
brinyiczki
kérdése
315
Sziasztok 2 feladatot csatoltam képbe nem tudom hogy kéne levezetni valaki tud segíteni?
Jelenleg 1 felhasználó nézi ezt a kérdést.
sos, matek, kérdés
sos, matek, kérdés
0
Középiskola / Matematika
Válaszok
1 kormosmate2
megoldása
kormosmate2
megoldása
1.)
` 2\cos(x-\frac{\pi}{3}) = -1 \text{/}:2 `
` \cos(x-\frac{\pi}{3}) = -\frac{1}{2} \text{/}\cos^{-1}() `
A koszinusznak két megoldás halmaza is van, az egyiket a számológép adja (vagy tudjuk mert nevezetes érték) a másikat úgy kapjuk, hogy 360°-ból levonjuk az elsőt (viszont radiánban számolunk, mert az egyenletben is radiánban vannak a szögek). Továbbá mindkét megoldás végtelenszer ismétlődik a koszinusz periódikussága miatt.
I.
` x-\frac{\pi}{3} = \frac{2\pi}{3}+k\cdot 2\pi \text{/}+\frac{\pi}{3} \Rightarrow x=\pi+k\cdot 2\pi\quad k\in\mathbb{Z}`
II.
` x-\frac{\pi}{3}=\frac{4\pi}{3}+l\cdot 2\pi \text{/} +\pi/3 \Rightarrow x = (5\pi)/3+l\cdot 2\pi\quad l\in\mathbb{Z}`
2.)
` 2\sin(2x) = -\sqrt{2} \text{/}:2 `
` \sin(2x) = -(\sqrt{2})/2 \text{/}\sin^{-1}() `
A szinusz hasonlóan viselkedik mint a koszinusz, viszont ott csak 180°-ból kell levonni az első megoldást. Arra kell még itt ügyelni, hogy amikor osztunk 2-vel, akkor a periódust is osztani kell!
I.
` 2x = -(\pi)/4+k\cdot 2\pi \text{/}:2 \Rightarrow x=-(\pi)/8+k\cdot \pi\quad k\in\mathbb{Z} `
I.
` 2x = (5\pi)/4+l\cdot 2\pi \text{/}:2 \Rightarrow x=(5\pi)/8+l\cdot \pi\quad l\in\mathbb{Z} `
` 2\cos(x-\frac{\pi}{3}) = -1 \text{/}:2 `
` \cos(x-\frac{\pi}{3}) = -\frac{1}{2} \text{/}\cos^{-1}() `
A koszinusznak két megoldás halmaza is van, az egyiket a számológép adja (vagy tudjuk mert nevezetes érték) a másikat úgy kapjuk, hogy 360°-ból levonjuk az elsőt (viszont radiánban számolunk, mert az egyenletben is radiánban vannak a szögek). Továbbá mindkét megoldás végtelenszer ismétlődik a koszinusz periódikussága miatt.
I.
` x-\frac{\pi}{3} = \frac{2\pi}{3}+k\cdot 2\pi \text{/}+\frac{\pi}{3} \Rightarrow x=\pi+k\cdot 2\pi\quad k\in\mathbb{Z}`
II.
` x-\frac{\pi}{3}=\frac{4\pi}{3}+l\cdot 2\pi \text{/} +\pi/3 \Rightarrow x = (5\pi)/3+l\cdot 2\pi\quad l\in\mathbb{Z}`
2.)
` 2\sin(2x) = -\sqrt{2} \text{/}:2 `
` \sin(2x) = -(\sqrt{2})/2 \text{/}\sin^{-1}() `
A szinusz hasonlóan viselkedik mint a koszinusz, viszont ott csak 180°-ból kell levonni az első megoldást. Arra kell még itt ügyelni, hogy amikor osztunk 2-vel, akkor a periódust is osztani kell!
I.
` 2x = -(\pi)/4+k\cdot 2\pi \text{/}:2 \Rightarrow x=-(\pi)/8+k\cdot \pi\quad k\in\mathbb{Z} `
I.
` 2x = (5\pi)/4+l\cdot 2\pi \text{/}:2 \Rightarrow x=(5\pi)/8+l\cdot \pi\quad l\in\mathbb{Z} `
Módosítva: 3 éve
1
- Még nem érkezett komment!