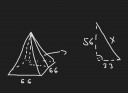Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Valaki tudna segíteni csonkagúla kiszámolásában?
 artep6
kérdése
artep6
kérdése
273
Nem tudok rájönni erre a három feladatra
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 kormosmate2
megoldása
kormosmate2
megoldása
52) a) A képen látható a gúla. A belsejébe berajzolt derékszögű háromszög átfogója Pitagorasz tétellel számolható. A rövidebbik befogó azért 33, mert az éppen az alap négyzet középvonalának a fele.
` x = \sqrt{56^2+33^2} = 65 `
Mivel szabályos a gúla, a palást négy ugyanolyan háromszögből áll, ezeknek előbb számoltuk ki a magasságát. A felszínt az alapterület és a palást területe adja:
` A=66^2+4\cdot \frac{66\cdot 65}{2} = 12 936\quad cm^2`
b) Ha a feladatlap illusztrációjának megfelelő módon félbevágjuk a gúlát, akkor a csonkagúla tetején keletkező kisebb négyzet éle éppen az oldallapi háromszög középvonala, tehát az alapél fele, azaz 33 cm.
Csonkagúla térfogata: ` V=\frac{m(t+\sqrt{t\cdot T}+T)}{3} ` ahol m a gúla magassága, t és T pedig rendre a kis és nagy négyzet területe. Így ` V=\frac{56(33^2+\sqrt{33^2\cdot 66^2}+66^2)}{3} = 142 296\quad cm^3`
A gráfos feladatrész többi része nem látszik, így azt nem tudom leírni.
17.3. Könnyen belátható, hogy a felül keletkező kis háromszög élei éppen harmada az alapháromszög éleinek. Szabályos háromszög lévén, a terület számolható így: ` T=a^2\frac{\sqrt{3}}{4} ` ahol `a` a háromszög oldalhossza. Így az alapháromszög területe: ` T=6^2\frac{\sqrt{3}}{4}= 9\sqrt{3}` A felső kis háromszög hasonló az alsóhoz, mivel minden szögük megegyezik. A területek négyzetesen arányosak, ezért ha az oldalai harmadakkorák az alapháromszögének, akkor a területe kilenced akkora lesz mint az alsóé, azaz ` t=\sqrt{3}`. A gúla térfogata hasonlóan az előzőhöz: ` V=\frac{9((\sqrt{3})^2+\sqrt{(\sqrt{3})^2\cdot(9\sqrt{3})^2}+(9\sqrt{3})^2)}{3} = 819\quad cm^3 `
17.5. Szinte teljesen ugyanaz mint az előbb, csak most ötszög alapú csonkagúlánk van, ezért egy kicsit többet kell számolni. Az alsó és felső ötszög most is hasonlóak. A hasonlóság aránya az oldalak miatt `\lambda = \frac{4}{6} = \frac{2}{3} ` így a területeknél ` \lambda^2=\frac{4}{9} `. Most számoljuk az alapötszög területét. Ezt úgy csináljuk, hogy feldaraboljuk a középpontja körül 5 egybevágó egyenlőszárú háromszögre, és egy ilyennek kiszámoljuk a területét majd azt vesszük 5-ször. Vegyük az egyik ilyen háromszöget. A szögszára a 360° ötödrésze, azaz 72°. Ha ezt a háromszöget a szimmetriatengelye mentén elfelezzük, akkor egy derékszőgú háromszöget kapunk, melyben van egy 36°-os szög, az azzal szemközti befogó az alapél fele, azaz 3 cm. Innen kétféle úton is folytathatjuk. Vagy kiszámoljuk a másik befogót, ami a háromszög magassága, és számolunk az alap*magasság/2 képlettel, vagy kiszámoljuk az átfogót, ami a két egyenlő szár közül az egyik, és az ` \frac{ab\sin \gamma}{2} ` képlettel számoljuk a területet. Mindkét esetben trigonometriával számolhatjuk az ismeretlen oldalt (tangens, szinusz). Mindkétféleképpen azt kapjuk az ötszög területére, hogy ` 61.9372\quad cm^2 `. A felső ötszög területe így ` \frac{4}{9}\cdot 61.9372 = 27.5276\quad cm^2`
A szokásos csonkagúla képlettel, felhasználva, hogy a magasság 20 cm: ` 871.7082\quad cm^3`
Mivel ` 1\quad cm^3 = 1\quad ml ` így ` 8.717\quad dl ` víz fér a vázába.
` x = \sqrt{56^2+33^2} = 65 `
Mivel szabályos a gúla, a palást négy ugyanolyan háromszögből áll, ezeknek előbb számoltuk ki a magasságát. A felszínt az alapterület és a palást területe adja:
` A=66^2+4\cdot \frac{66\cdot 65}{2} = 12 936\quad cm^2`
b) Ha a feladatlap illusztrációjának megfelelő módon félbevágjuk a gúlát, akkor a csonkagúla tetején keletkező kisebb négyzet éle éppen az oldallapi háromszög középvonala, tehát az alapél fele, azaz 33 cm.
Csonkagúla térfogata: ` V=\frac{m(t+\sqrt{t\cdot T}+T)}{3} ` ahol m a gúla magassága, t és T pedig rendre a kis és nagy négyzet területe. Így ` V=\frac{56(33^2+\sqrt{33^2\cdot 66^2}+66^2)}{3} = 142 296\quad cm^3`
A gráfos feladatrész többi része nem látszik, így azt nem tudom leírni.
17.3. Könnyen belátható, hogy a felül keletkező kis háromszög élei éppen harmada az alapháromszög éleinek. Szabályos háromszög lévén, a terület számolható így: ` T=a^2\frac{\sqrt{3}}{4} ` ahol `a` a háromszög oldalhossza. Így az alapháromszög területe: ` T=6^2\frac{\sqrt{3}}{4}= 9\sqrt{3}` A felső kis háromszög hasonló az alsóhoz, mivel minden szögük megegyezik. A területek négyzetesen arányosak, ezért ha az oldalai harmadakkorák az alapháromszögének, akkor a területe kilenced akkora lesz mint az alsóé, azaz ` t=\sqrt{3}`. A gúla térfogata hasonlóan az előzőhöz: ` V=\frac{9((\sqrt{3})^2+\sqrt{(\sqrt{3})^2\cdot(9\sqrt{3})^2}+(9\sqrt{3})^2)}{3} = 819\quad cm^3 `
17.5. Szinte teljesen ugyanaz mint az előbb, csak most ötszög alapú csonkagúlánk van, ezért egy kicsit többet kell számolni. Az alsó és felső ötszög most is hasonlóak. A hasonlóság aránya az oldalak miatt `\lambda = \frac{4}{6} = \frac{2}{3} ` így a területeknél ` \lambda^2=\frac{4}{9} `. Most számoljuk az alapötszög területét. Ezt úgy csináljuk, hogy feldaraboljuk a középpontja körül 5 egybevágó egyenlőszárú háromszögre, és egy ilyennek kiszámoljuk a területét majd azt vesszük 5-ször. Vegyük az egyik ilyen háromszöget. A szögszára a 360° ötödrésze, azaz 72°. Ha ezt a háromszöget a szimmetriatengelye mentén elfelezzük, akkor egy derékszőgú háromszöget kapunk, melyben van egy 36°-os szög, az azzal szemközti befogó az alapél fele, azaz 3 cm. Innen kétféle úton is folytathatjuk. Vagy kiszámoljuk a másik befogót, ami a háromszög magassága, és számolunk az alap*magasság/2 képlettel, vagy kiszámoljuk az átfogót, ami a két egyenlő szár közül az egyik, és az ` \frac{ab\sin \gamma}{2} ` képlettel számoljuk a területet. Mindkét esetben trigonometriával számolhatjuk az ismeretlen oldalt (tangens, szinusz). Mindkétféleképpen azt kapjuk az ötszög területére, hogy ` 61.9372\quad cm^2 `. A felső ötszög területe így ` \frac{4}{9}\cdot 61.9372 = 27.5276\quad cm^2`
A szokásos csonkagúla képlettel, felhasználva, hogy a magasság 20 cm: ` 871.7082\quad cm^3`
Mivel ` 1\quad cm^3 = 1\quad ml ` így ` 8.717\quad dl ` víz fér a vázába.
Módosítva: 2 éve
1
- Még nem érkezett komment!