Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Kombinatorika
 monika-korcz8043
kérdése
monika-korcz8043
kérdése
810
1). Hány 5-jegyű szám van a 6-os számrendszerben? (a számjegyek: 0, 1, 2, 3, 4, 5) (4p)
2). Határozzuk meg az 1, 2, 2, 3, 3, 3 elemek permutációinak számát. Ezek között hány olyan van, amelyben az első helyen a 2 számjegy áll?
3). A 32 lapos magyar kártyából leosztottunk négy lapot. Hány darab, pontosan két ászt tartalmazó leosztás lehetséges?
4). 20 fehér és 10 piros rózsából hányféleképpen lehet 3 fehér és 4 piros rózsát tartalmazó csokrot készteni?
5). A városi középiskolás egyéni teniszbajnokság egyik csoportjába hatan kerültek: András, Béla, Csaba, Dani, Ede és
Feri. A versenykiírás szerint bármely két fiúnak pontosan egyszer kell játszania egymással. Eddig András már játszott
Bélával, Danival és Ferivel. Béla játszott már Edével is. Csaba csak Edével játszott, Dani pedig Andráson kívül csak
Ferivel. Ede és Feri egyaránt két mérkőzésen van túl.
a) Szemléltesse gráffal a lejátszott mérkőzéseket! (3p)
b) Hány mérkőzés van még hátra? (4p)
c) Hány olyan sorrend alakulhat ki, ahol a hat versenyző közül Dani az első két hely valamelyikén végez?
2). Határozzuk meg az 1, 2, 2, 3, 3, 3 elemek permutációinak számát. Ezek között hány olyan van, amelyben az első helyen a 2 számjegy áll?
3). A 32 lapos magyar kártyából leosztottunk négy lapot. Hány darab, pontosan két ászt tartalmazó leosztás lehetséges?
4). 20 fehér és 10 piros rózsából hányféleképpen lehet 3 fehér és 4 piros rózsát tartalmazó csokrot készteni?
5). A városi középiskolás egyéni teniszbajnokság egyik csoportjába hatan kerültek: András, Béla, Csaba, Dani, Ede és
Feri. A versenykiírás szerint bármely két fiúnak pontosan egyszer kell játszania egymással. Eddig András már játszott
Bélával, Danival és Ferivel. Béla játszott már Edével is. Csaba csak Edével játszott, Dani pedig Andráson kívül csak
Ferivel. Ede és Feri egyaránt két mérkőzésen van túl.
a) Szemléltesse gráffal a lejátszott mérkőzéseket! (3p)
b) Hány mérkőzés van még hátra? (4p)
c) Hány olyan sorrend alakulhat ki, ahol a hat versenyző közül Dani az első két hely valamelyikén végez?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 kormosmate2
megoldása
kormosmate2
megoldása
1) Az első helyre nem tehetjük a 0 számjegyet, a többi helyre viszont már bármelyik számjegy mehet, így 5*6⁴=6480
2) Ez ismétléses permutáció, mivel vannak egymástól megkülönböztethetlen elemek. Van két db 2-esünk és 3 darab 3-asunk, így a lehetséges permutációk száma: ` P_6^{2,3(i)}=\frac{6!}{2!*3!}=60 `
Ha az első helyre lefixáljuk az egyik kettest, akkor már csak 5 db számot permutálunk, köztük 3 db hármassal: ` P_5^{3(i)}=\frac{5!}{3!} = 20 `
3) A sorrend nem számít csak az, hogy 2 db ászunk legyen, így ez kombináció. Hányféleképpen lehet 2 ászt választani a 4 ász közül, amihez még kell választani 2 kártyát a maradék 28-ből ami nem ász: ` C_4^2\cdot C_28^2 = ((4),(2))\cdot ((28),(2)) = 2268 `
4) A rózsaszálakat kiválasztjuk a csokorba, a sorrend nem számít, így ez megint kombináció:
3 fehér és 4 piros rózsát kell választani: ` C_20^3\cdot C_10^4=((20),(3))\cdot ((10),(4)) = 239400 `
5)
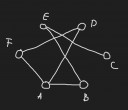
a) A gráf egy-egy csúcsának megfeleltetünk egy játékost, így egy 6 csúcsú gráfunk van. A játékosok kezdőbetűivel jelöljük a csúcsokat. Ha két játékos játszott egymással, akkor az őket jelentő csúcsokat éllel kötjük össze. Csatolt képen a gráf.
b) Ha mindenki mindenkivel egyszer játszik, akkor a játék végén az összes élt be kellene rajzolnunk. Egy ` n ` pontú teljes gráf összes éleinek száma: ` \frac{n(n-1)}{2} ` mivel minden csúcsből csak önmagába nem húzható él és minden élt kétszer is megszámoltunk a két végén. Most egy 6 pontú gráfunk van, így az összes él száma 15. Eddig 6 mérkőzést játszottak le, így még 9 van hátra.
c) Danit rögzítjük az első vagy a második helyre, a többiek a maradék helyezésekre mindkét esetben ` 5! ` féleképpen kerülhetnek. Így ` 5!*2=240 ` féle sorrend lehetséges.
2) Ez ismétléses permutáció, mivel vannak egymástól megkülönböztethetlen elemek. Van két db 2-esünk és 3 darab 3-asunk, így a lehetséges permutációk száma: ` P_6^{2,3(i)}=\frac{6!}{2!*3!}=60 `
Ha az első helyre lefixáljuk az egyik kettest, akkor már csak 5 db számot permutálunk, köztük 3 db hármassal: ` P_5^{3(i)}=\frac{5!}{3!} = 20 `
3) A sorrend nem számít csak az, hogy 2 db ászunk legyen, így ez kombináció. Hányféleképpen lehet 2 ászt választani a 4 ász közül, amihez még kell választani 2 kártyát a maradék 28-ből ami nem ász: ` C_4^2\cdot C_28^2 = ((4),(2))\cdot ((28),(2)) = 2268 `
4) A rózsaszálakat kiválasztjuk a csokorba, a sorrend nem számít, így ez megint kombináció:
3 fehér és 4 piros rózsát kell választani: ` C_20^3\cdot C_10^4=((20),(3))\cdot ((10),(4)) = 239400 `
5)
a) A gráf egy-egy csúcsának megfeleltetünk egy játékost, így egy 6 csúcsú gráfunk van. A játékosok kezdőbetűivel jelöljük a csúcsokat. Ha két játékos játszott egymással, akkor az őket jelentő csúcsokat éllel kötjük össze. Csatolt képen a gráf.
b) Ha mindenki mindenkivel egyszer játszik, akkor a játék végén az összes élt be kellene rajzolnunk. Egy ` n ` pontú teljes gráf összes éleinek száma: ` \frac{n(n-1)}{2} ` mivel minden csúcsből csak önmagába nem húzható él és minden élt kétszer is megszámoltunk a két végén. Most egy 6 pontú gráfunk van, így az összes él száma 15. Eddig 6 mérkőzést játszottak le, így még 9 van hátra.
c) Danit rögzítjük az első vagy a második helyre, a többiek a maradék helyezésekre mindkét esetben ` 5! ` féleképpen kerülhetnek. Így ` 5!*2=240 ` féle sorrend lehetséges.
Módosítva: 3 éve
0
- Még nem érkezett komment!