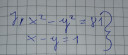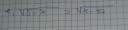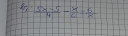Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Másodfokú egyenlet
 Tóth Márton
kérdése
Tóth Márton
kérdése
279
Sziasztok az egyenletek megoldása kéne mert nem tudom megoldani.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
4 RationalRick
{ Fizikus }
megoldása
RationalRick
{ Fizikus }
megoldása
Egyesével küldöm őket.
b)
`(5x-5)/4-x/6=6/x` `//*24x`
`x≠0`
`6x(5x-5)-4x^2=144`
`30x^2-30x-4x^2-144=0`
`26x^2-30x-144=0`
Megoldóképlet:
`x_1=-24/13`
`x_2=3`
Egyik se 0, ekvivalensek voltak átalakítások, tehát jók a kapott gyökök.
`M={-24/13; 3}`
b)
`(5x-5)/4-x/6=6/x` `//*24x`
`x≠0`
`6x(5x-5)-4x^2=144`
`30x^2-30x-4x^2-144=0`
`26x^2-30x-144=0`
Megoldóképlet:
`x_1=-24/13`
`x_2=3`
Egyik se 0, ekvivalensek voltak átalakítások, tehát jók a kapott gyökök.
`M={-24/13; 3}`
1
- Még nem érkezett komment!
 RationalRick
{ Fizikus }
válasza
RationalRick
{ Fizikus }
válasza
`e)`
`sqrt(5-x)=sqrt(x-10)`
Mivel a négyzetre emelés nem ekvivalens átalakítás, ezért vagy kell kikötést tenni, vagy ellenőrízni kell. Én most mindkettőt megcsinálom.
Kikötés:
`5-x≥0`
`x≤5`
és
`x-10≥0`
`x≥10`
De hát a kettő nem lehet egyszerre igaz, szóval már most látszik, hogy nincs megoldás. De most megcsinálom ellenőrzéssel is:
`sqrt(5-x)=sqrt(x-10)` `//^2`
`5-x=x-10`
`2x=15`
`x=15/2`
Ellenőrzés:
Baloldal:
`sqrt(5-15/2)=sqrt(-5/2)` Ez eleve nem jó, mert negatív számoknak nincs valós gyökem
Jobboldal:
`sqrt(15/2-10)=sqrt(-5/2)` ugyanez a helyzet
Tehát nincs megoldás.
`sqrt(5-x)=sqrt(x-10)`
Mivel a négyzetre emelés nem ekvivalens átalakítás, ezért vagy kell kikötést tenni, vagy ellenőrízni kell. Én most mindkettőt megcsinálom.
Kikötés:
`5-x≥0`
`x≤5`
és
`x-10≥0`
`x≥10`
De hát a kettő nem lehet egyszerre igaz, szóval már most látszik, hogy nincs megoldás. De most megcsinálom ellenőrzéssel is:
`sqrt(5-x)=sqrt(x-10)` `//^2`
`5-x=x-10`
`2x=15`
`x=15/2`
Ellenőrzés:
Baloldal:
`sqrt(5-15/2)=sqrt(-5/2)` Ez eleve nem jó, mert negatív számoknak nincs valós gyökem
Jobboldal:
`sqrt(15/2-10)=sqrt(-5/2)` ugyanez a helyzet
Tehát nincs megoldás.
1
- Még nem érkezett komment!
 RationalRick
{ Fizikus }
válasza
RationalRick
{ Fizikus }
válasza
j)
`x^2-y^2=81`
`x-y=1`
Az alsó egyenletből kifejezem az `x`-et:
`x=y+1`
Behelyettesítem a másikba:
`(y+1)^2-y^2=81`
`y^2+2y+1-y^2=81`
`2y+1=81`
`2y=82`
`y=41`
És akkor
`x=41-1=40`
Ellenőrzés:
`41^2-40^2=81`
`81=81`
`41-40=1`
`1=1`
`M={(41, 40)}`
`x^2-y^2=81`
`x-y=1`
Az alsó egyenletből kifejezem az `x`-et:
`x=y+1`
Behelyettesítem a másikba:
`(y+1)^2-y^2=81`
`y^2+2y+1-y^2=81`
`2y+1=81`
`2y=82`
`y=41`
És akkor
`x=41-1=40`
Ellenőrzés:
`41^2-40^2=81`
`81=81`
`41-40=1`
`1=1`
`M={(41, 40)}`
1
-
Tóth Márton: Köszönöm az összeset 3 éve 0
-
RationalRick: Szívesen! Megoldásnak jelölést elfogadok!
 3 éve
0
3 éve
0
 RationalRick
{ Fizikus }
válasza
RationalRick
{ Fizikus }
válasza
c)
`(17+2x)/(x+3)-6/(x^2-9)-2/(x-3)=(3x+7)/(3-x)`
`x≠3` és `x≠-3`
`(17+2x)/(x+3)-6/(x^2-9)-2/(x-3)=(3x+7)/(3-x)` `//*(x^2-9)`
`(17+2x)(x-3)-6-2(x+3)=-(3x+7)(x+3)`
`(17+2x)(x-3)-6-2(x+3)+(3x+7)(x+3)=0`
`17x-51+2x^2-6x-6-2x-6+3x^2+9x+7x+21=0`
`5x^2+25x-42=0`
Megoldóképlet:
`x_1=(-25-sqrt(1465))/10`
`x_2=(-25+sqrt(1465))/10`
Ezek elég csúnya megoldások, de hát ez volt a feladat...
`(17+2x)/(x+3)-6/(x^2-9)-2/(x-3)=(3x+7)/(3-x)`
`x≠3` és `x≠-3`
`(17+2x)/(x+3)-6/(x^2-9)-2/(x-3)=(3x+7)/(3-x)` `//*(x^2-9)`
`(17+2x)(x-3)-6-2(x+3)=-(3x+7)(x+3)`
`(17+2x)(x-3)-6-2(x+3)+(3x+7)(x+3)=0`
`17x-51+2x^2-6x-6-2x-6+3x^2+9x+7x+21=0`
`5x^2+25x-42=0`
Megoldóképlet:
`x_1=(-25-sqrt(1465))/10`
`x_2=(-25+sqrt(1465))/10`
Ezek elég csúnya megoldások, de hát ez volt a feladat...
1
- Még nem érkezett komment!