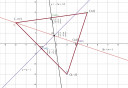
A(-2;2) , B(3;-3) , C(5;3)

Kellenek hozzá az oldalak meredeksége és az oldalfelező pontok.

`m_(AB)` = `(y_B-y_A)/(x_B-x_A)` = `(-3-2)/(3-(-2))` = `-5/5` = -1

Az oldalfelező merőleges meredeksége:

`m(OF)_(AB)` = `-1/m_(AB)` = 1

`F(AB)` = `(x_B+x_A)/2;(y_B+y_A)/2)` = `(3+(-2))/2;(-3+2)/2` = `(1/2;-1/2)`

Ha ismerjük egy egyenes pontját és a meredekségét, akkor fel tudjuk írni az egyenletét:

`y_F(AB)=m(OF)_(AB)*x_F(AB)+b_(AB)`

`-1/2=1*1/2+b_(AB)`

`b_(AB)=-1`

Az egyik oldalfelező merőleges egyenlete:

`color(red)(y=x-1)`

II.

`m_(AC)=(y_C-y_A)/(x_C-x_A)` = `(3-2)/(5-(-2))` = `1/7`

A felezőmerőlegesé: `m(OF)_(AC)=-1/m_(AC)` = -7

`F(AC)`: `(x_C+x_A)/2;(y_C+y_A)/2` : `(5+(-2))/2;(3+2)/2` : `(3/2;5/2)`

`y_F(AC)=m(OF)_(AC)*x_F(AC)+b_(AC)`

`5/2=(-7)*3/2+b_(AC)`

`b_(AC)=5/2+21/2` = 13

A másik oldalfelező merőleges egyenlete:

`color(red)(y=-7x+13)`

III.

`m_(BC)=(y_C-y_B)/(x_C-x_B)` = `(3-(-3))/(5-3)` = `6/2` = 3

A felezőmerőlegesé: `m(OF)_(BC)=-1/m_(BC)` = `-1/3`

`F(BC)` : `(x_C+x_B)/2;(y_C+y_B)/2` : `(5+3)/2;(3+(-3))/2` : `(4;0)`

`y_F(BC)=m(OF)_(BC)*x_F(BC)+b_(BC)`

`0=-1/3*4+b_(BC)`

`b_(BC)=4/3`

A harmadik oldalfelező merőleges egyenlete:

`color(red)(y=-1/3*x+4/3)` vagy felírhatod így: `3y+x=4`

b,

Ha behelyettesítjük az adott pontot mindhárom egyenletbe és azonosságot kapunk, akkor a pont illeszkedik mindhárom egyenesre.

`O(7/4;3/4)`

I. `3/4=7/4-1`

II. `3/4=(-7)*7/4+13`

III. `3/4=-1/3*7/4+4/3`

c,

Az oldalfelező merőlegesek egyenlő távolságra vannak a csúcsoktól. Két oldalfelező merőleges metszéspontja egyenlő távolságra van mindhárom csúcstól. Ez a pont a háromszög köré írható kör középpontja.

`d_(OA)=root()((x_O-x_A)^2+(y_O-y_A)^2)` = `root()((7/4-(-2))^2+(3/4-2)^2)` = `root()((15/4)^2+(-5/4)^2)` = `root()(250)/4`

`d_(OB)=root()((x_O-x_B)^2+(y_O-y_B)^2)` = `root()((7/4-3)^2+(3/4-(-3))^2)` = `root()((-5/4)^2+(15/4)^2)` = `root()(250)/4`

`d_(OC)=root()(x_O-x_C)^2+(y_O-y_C)^2)` = `root()((7/4-5)^2+(3/4-3)^2)` = `root()((-13/4)^2+(-9/4)^2)` = `root()(250)/4` = `5/4*root()(10)`