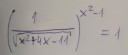Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Exponenciális egyenlet
 Törölt
kérdése
Törölt
kérdése
296
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 kazah
válasza
kazah
válasza
Felt:
`x^2+4x-11 gt 0`
`(x+2)^2-4-11 gt 0`
`(x+2)^2-15 gt 0`
`(x+2)^2 gt 15`
`-2-root()(15) lt x` és `x gt root()(15)-2`
A megoldás(oka)t az alábbi halmazon keressük:
`x in RR`, `x in ]-oo;-2-root()(15)[ cup ]root()(15)-2;oo[` (-5,87-nél kisebb és 1,87-nél nagyobb)
Egy hatványkifejezés akkor 1, ha:
I. a kitevő nulla:
`x^2-1=0`
`x^2=1`
`x_1=-1` ; `x_2=1` ; a kezdezi feltételeknek ezek nem felelnek meg.
II. Ha az alap értéke 1.
`1/root()(x^2+4x-11)=1`
`x^2+4x-11=1`
`x^2+4x-12=0`
(vagy megoldóképlet)
`(x+6)(x-2)=0`
`x_3=-6` Megfelel a kezdeti feltételnek.
`x_4=2` Ez is.
Megoldás: x = -6 és x=2.
`x^2+4x-11 gt 0`
`(x+2)^2-4-11 gt 0`
`(x+2)^2-15 gt 0`
`(x+2)^2 gt 15`
`-2-root()(15) lt x` és `x gt root()(15)-2`
A megoldás(oka)t az alábbi halmazon keressük:
`x in RR`, `x in ]-oo;-2-root()(15)[ cup ]root()(15)-2;oo[` (-5,87-nél kisebb és 1,87-nél nagyobb)
Egy hatványkifejezés akkor 1, ha:
I. a kitevő nulla:
`x^2-1=0`
`x^2=1`
`x_1=-1` ; `x_2=1` ; a kezdezi feltételeknek ezek nem felelnek meg.
II. Ha az alap értéke 1.
`1/root()(x^2+4x-11)=1`
`x^2+4x-11=1`
`x^2+4x-12=0`
(vagy megoldóképlet)
`(x+6)(x-2)=0`
`x_3=-6` Megfelel a kezdeti feltételnek.
`x_4=2` Ez is.
Megoldás: x = -6 és x=2.
0
- Még nem érkezett komment!