Keresés


Toplista

Toplista
  • betöltés...

Magántanár kereső

Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!

Határérték 11

143
Határozzuk meg a `lim_(x->0)(cosx-1)/x^2` határértékét.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika

Válaszok

2
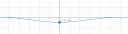
Az előttem szóló megoldása is jó természetesen, csak matematikailag helytelen a levezetés. Én ábrázoltam is azért, hogy elhidd :P
Válasz kép
Válasz kép
Módosítva: 1 éve
0

`lim_(x rightarrow 0)(cosx-1)/x^2` = `lim_(x rightarrow 0)(cosx-1)/x^2*(cosx+1)/(cosx+1)` = `lim_(x rightarrow 0)(cos^2x-1)/(x^2*(cosx+1))` = `lim_(x rightarrow 0)-(1-cos^2x)/(x^2*(cosx+1))` = `lim_(x rightarrow 0)-(sinx/x)^2*lim_(x rightarrow 0)(1/(cosx+1))` = `-(1^2)*1/(1+1)` = `-1/2`
0