Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
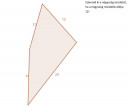
Valaki le tudná vezetni nekem ezt a geometriai feladatot?
 Benedek Balázs
kérdése
Benedek Balázs
kérdése
318
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 peristvan
megoldása
peristvan
megoldása
Behúzva a négyszög rövidebbik átlóját a két keletkező háromszög terület összege fogja adni a négyszög területét. Ehhez kell az egyes háromszögekben ismert oldalak segítségével valamelyik szög kiszámolása, melyet cosinus tétellel lehet kiszámolni. Majd ha ez a szög megvan, akkor a háromszög területét a sinusos képlettel lehet kiszámolni (két oldal és közbezárt szögük szinuszának szorzatát felezve).
A keletkező fenti háromszög két 12 egység hosszú oldalai közötti szöget (alfát) kiszámolhatjuk cosinus tétellel:
132 = 122 + 122 - 2 * 12 * 12 * cos (alfa) / - 2*122
169 - 288 = -288 * cos (alfa) /: (-288)
cos (alfa) = -119 / (-288) = 0,4132, melyből alfa = 65,59o
T(fenti háromszög) = 12 * 12 * sin 65,59o : 2 =65,57 (e2)
A keletkező lenti háromszög 14 és 20 egység hosszú oldalai közötti szöget (bétát) kiszámolhatjuk cosinus tétellel:
122 = 142 + 202 - 2 * 14 * 20 * cos (béta) / - 142 - 202
144 - 196 - 400 = -560 * cos (béta) /: (-560)
cos (alfa) = -452 / (-560) = 0,8071, melyből béta= 36,18o
T(lenti háromszög) = 14 * 20 * sin 36,18 o : 2 =82,65 (e2)
Tehát a teljes négyszög területe:
65,57 + 82,65 =148,22 (e2)
A keletkező fenti háromszög két 12 egység hosszú oldalai közötti szöget (alfát) kiszámolhatjuk cosinus tétellel:
132 = 122 + 122 - 2 * 12 * 12 * cos (alfa) / - 2*122
169 - 288 = -288 * cos (alfa) /: (-288)
cos (alfa) = -119 / (-288) = 0,4132, melyből alfa = 65,59o
T(fenti háromszög) = 12 * 12 * sin 65,59o : 2 =65,57 (e2)
A keletkező lenti háromszög 14 és 20 egység hosszú oldalai közötti szöget (bétát) kiszámolhatjuk cosinus tétellel:
122 = 142 + 202 - 2 * 14 * 20 * cos (béta) / - 142 - 202
144 - 196 - 400 = -560 * cos (béta) /: (-560)
cos (alfa) = -452 / (-560) = 0,8071, melyből béta= 36,18o
T(lenti háromszög) = 14 * 20 * sin 36,18 o : 2 =82,65 (e2)
Tehát a teljes négyszög területe:
65,57 + 82,65 =148,22 (e2)
1
-
Benedek Balázs: Nagyon szépen köszönöm 3 éve 0