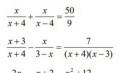Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Hogy kéne ezt a két törtes másodfokú egyenletet megoldani?
 Tory___
kérdése
Tory___
kérdése
326
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 -O-
{ Fizikus }
megoldása
-O-
{ Fizikus }
megoldása
1. feladat:
1) Értelmezési tartomány: `x!=4`; `x!=-4`
Közös nevezőre hozzuk a két törtet. Ez `(x-4)*(x+4)`.
`(x*(x-4))/((x-4)*(x+4))+(x*(x+4))/((x-4)*(x+4))=50/9`
`(x^2-4x+x^2+4x)/((x-4)*(x+4))=50/9`
`(2x^2)/(x^2-16)=50/9`
Szorozzunk keresztbe.
`18x^2=50x^2-50*16`
`32x^2=800`
`x^2=25`
`x_(1,2)=+-5`
2. feladat:
Értelmezési tartomány: `x!=-4`; `x!=3`.
Alakítsuk egy kicsit át a második tört nevezőjét: a `3-x=-x+3` kifejezésből emeljünk ki `-1`-et, így `-(x-3)` lesz belőle. A `-` jel a tört előtti kivonás jelet összeadás jellé változtatja.
`(x+3)/(x+4)+x/(x-3)=7/((x+4)*(x-3)`
Közös nevező: `(x+4)*(x-3)`
`((x+3)*(x-3)+x*(x+4))/((x+4)*(x-3))=7/((x+4)*(x-3)`
Vonjuk ki a jobb oldalt.
`((x+3)*(x-3)+x*(x+4)-7)/((x+4)*(x-3))=0`
`(x^2-9+x^2+4x-7)/((x+4)*(x-3))=0`
`(2x^2+4x-16)/(x^2+x-12)=0`
Egy kifejezés akkor nulla, ha a számlálója nulla.
Ennek fényében:
`2x^2+4x-16=0`
Másodfokú megoldóképletből: `x_1=-4; x_2=2`
Az értelmezési tartomány miatt az első gyök nem elfogadható. Így a megoldás: `x=2`.
1) Értelmezési tartomány: `x!=4`; `x!=-4`
Közös nevezőre hozzuk a két törtet. Ez `(x-4)*(x+4)`.
`(x*(x-4))/((x-4)*(x+4))+(x*(x+4))/((x-4)*(x+4))=50/9`
`(x^2-4x+x^2+4x)/((x-4)*(x+4))=50/9`
`(2x^2)/(x^2-16)=50/9`
Szorozzunk keresztbe.
`18x^2=50x^2-50*16`
`32x^2=800`
`x^2=25`
`x_(1,2)=+-5`
2. feladat:
Értelmezési tartomány: `x!=-4`; `x!=3`.
Alakítsuk egy kicsit át a második tört nevezőjét: a `3-x=-x+3` kifejezésből emeljünk ki `-1`-et, így `-(x-3)` lesz belőle. A `-` jel a tört előtti kivonás jelet összeadás jellé változtatja.
`(x+3)/(x+4)+x/(x-3)=7/((x+4)*(x-3)`
Közös nevező: `(x+4)*(x-3)`
`((x+3)*(x-3)+x*(x+4))/((x+4)*(x-3))=7/((x+4)*(x-3)`
Vonjuk ki a jobb oldalt.
`((x+3)*(x-3)+x*(x+4)-7)/((x+4)*(x-3))=0`
`(x^2-9+x^2+4x-7)/((x+4)*(x-3))=0`
`(2x^2+4x-16)/(x^2+x-12)=0`
Egy kifejezés akkor nulla, ha a számlálója nulla.
Ennek fényében:
`2x^2+4x-16=0`
Másodfokú megoldóképletből: `x_1=-4; x_2=2`
Az értelmezési tartomány miatt az első gyök nem elfogadható. Így a megoldás: `x=2`.
Módosítva: 3 éve
0
- Még nem érkezett komment!