2408. Feladat

`V_("10 cm")=(4*r^3*pi)/3=(4*10^3*pi)/3=(4.000pi)/3 \ cm^3`

`V_("1 cm")=(4*r^3*pi)/3=(4*1^3*pi)/3=(4pi)/3 \ cm^3`

Jól látszik, hogy a nagy gömb térfogata 1000 szerese a kis gömbének így `color(red)(1.000)` darabot lehet önteni belőle.

`A_("10 cm")=4*r^2*pi=4*10^2*pi=400pi \ cm^2`

`A_("1 cm")=4*r^2*pi=4*1^2*pi=4pi \ cm^2`

Az összes golyó felszíne: `1.000 * 4pi=4.000pi \ cm^2` ami `(4.000pi)/(400pi)=color(red)(10)` szerese az eredeti gömbének.



2409. Feladat

`V_1=(4*r^3*pi)/3=(4*5^3*pi)/3=(500pi)/3 \ cm^3`

`V_2=(4*r^3*pi)/3=(4*8^3*pi)/3=(2.048pi)/3 \ cm^3`

`V_3=(4*r^3*pi)/3=(4*12^3*pi)/3=(6.912pi)/3 \ cm^3`

`V_("összes")=V_1+V_2+V_3=(500pi)/3 +(2.048pi)/3+(6.912pi)/3=(12.724pi)/3 \ cm^3`

`r_("nagy gömb")=root(3)((3V)/(4pi))=root(3)((3*(12.724pi)/3 )/(4pi))approxcolor(red)(14,71 \ cm)`



2410. Feladat
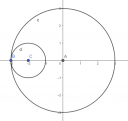
Csatoltam képet is.

Legyen a kisebb gömb sugara r a nagyobb gömb sugara pedig `R=r+2`.

A térfogatok segítségével írjuk fel a következő egyenletet:

`(4*(r+2)^3*pi)/3-(4*r^3*pi)/3=108,909`

`(4pir^3+24pir^2+48pir+32pi)/3-(4pir^3)/3=108,909`

`4pir^3+24pir^2+48pir+32pi-4pir^3=326,727`

`24pir^2+48pir+32pi=326,727`

`24pir^2+48pir+32pi-326,727=0`

`r_(1,2) = (-b+-sqrt(b^2-4ac))/(2a)=(-48pi+-sqrt((48pi)^2-4*24pi*(32pi-326,727)))/(2*24pi)={(cancel(r_1= "-3" \ "cm")) , (color(red)(r_2 = "1" \ "cm")):}`

Ezek alapján a kis kör sugara `r=color(red)(1 \ cm)` hosszúságú míg a nagyobbik kör sugara`R=r+2=1+2=color(red)(3 \ cm)` hosszúságú.