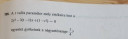Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matematika paraméteres egyenlet megoldása Viéte- formulával
 Luca123
kérdése
Luca123
kérdése
267
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 RationalRick
{ Fizikus }
megoldása
RationalRick
{ Fizikus }
megoldása
`2x^2-3(t-1)x+(1-t^2)=0`
Diszkriminánst megnézem:
`D=b^2-4ac`
`a=2`
`b=-3(t-1)`
`c=1-t^2`
`D=(-3(t-1))^2-4*2*(1-t^2)>=0`
`9t^2-18t+9-8+8t^2>=0`
`17t^2-18t+1>=0`
Zérushelyek: `x_1=1/17` `x_2=1`
Tehát erre értelmes:
`]-∞; 1/17]cup[1; ∞[`
Hogy is vannak a Viète-fromulák?
`x_1+x_2=-b/a`
`x_1*x_2=c/a`
Mi is az a négyzetösszeg?
`(x_1)^2+(x_2)^2`
átalakítva:
`(x_1+x_2)^2-2x_1*x_2`
Átírva Viète-fromulákra:
`(-b/a)^2-2*c/a`
És akkor az egyenlet:
`(-(-3(t-1))/2)^2-2*(1-t^2)/2=5/4`
`((-3t+3)^2)/4-1+t^2=5/4`
`(9t^2-18t+9)/4-1+t^2=5/4` `//*4`
`9t^2-+8t+9-4+4t^2=5`
`13t^2-18t=0`
`t(13t-18)=0`
`t_1=0`
`13t_2-18=0`
`13t_2=18`
`t_2=18/13`
Mindkettő benne van az értelmezési tartománynak, tehát megoldások.
Diszkriminánst megnézem:
`D=b^2-4ac`
`a=2`
`b=-3(t-1)`
`c=1-t^2`
`D=(-3(t-1))^2-4*2*(1-t^2)>=0`
`9t^2-18t+9-8+8t^2>=0`
`17t^2-18t+1>=0`
Zérushelyek: `x_1=1/17` `x_2=1`
Tehát erre értelmes:
`]-∞; 1/17]cup[1; ∞[`
Hogy is vannak a Viète-fromulák?
`x_1+x_2=-b/a`
`x_1*x_2=c/a`
Mi is az a négyzetösszeg?
`(x_1)^2+(x_2)^2`
átalakítva:
`(x_1+x_2)^2-2x_1*x_2`
Átírva Viète-fromulákra:
`(-b/a)^2-2*c/a`
És akkor az egyenlet:
`(-(-3(t-1))/2)^2-2*(1-t^2)/2=5/4`
`((-3t+3)^2)/4-1+t^2=5/4`
`(9t^2-18t+9)/4-1+t^2=5/4` `//*4`
`9t^2-+8t+9-4+4t^2=5`
`13t^2-18t=0`
`t(13t-18)=0`
`t_1=0`
`13t_2-18=0`
`13t_2=18`
`t_2=18/13`
Mindkettő benne van az értelmezési tartománynak, tehát megoldások.
0
-
Luca123: Nagyon szépen köszönöm! 3 éve 0
-
RationalRick: Nincs mit! Remélem, jól csináltam!
 3 éve
0
3 éve
0