Trigonometria

Az ábrák illusztráció jellegűek nem pontos méretek és szögek!

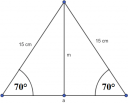
1. Feladat (1. kép)
a.)
Az első kép az.

b.)
`m=15*sin70°=color(red)(14,1 \ cm)`

c.)
`a=2*sqrt(15^2-14,1^2)=color(red)(10,24 \ cm)`



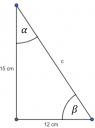
2. Feladat (2. kép)
`tgalpha=12/15`

`tgalpha=0,8`

`alpha=color(red)(38,66°)`


`tgbeta=15/12`

`tgbeta=1,25`

`beta=color(red)(51,34°)`



3. Feladat (3. kép)
Először is kiszámítjuk, a harmadik oldalt koszinusz tétel használatával majd a többi szöget könnyedén meghatározzuk szinusztétel alkalmazásával.

`c=sqrt(10^2+8^2-2*10*8*cos122°)=color(red)(15,77 \ cm)`

Alkalmazzuk most a szinusz tételt a változatosság kedvéért.

`sinalpha=(sin122°)/((15,77)/10)`

`sinalpha=0,5377`

`color(red)(alpha=32,52°)`


`sinbeta=(sin122°)/((15,77)/8)`

`sinbeta=0,4302`

`color(red)(beta=25,48°)`



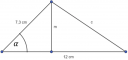
4. Feladat (4. kép)
A háromszög területe számítható `T=(a*m_a)/2` képlettel. Ebből tudjuk vissza vezetni a 12 cm-es oldalhoz tartozó magasságot melyel kapunk egy derékszögű háromszöget ahogy az ábrán is látható. Melyel meghatározzuk a hiányzó oldallal szemközti szöget hogy megtudjuk határozni a hiányzó oldalt koszinusztétel alkalmazásával.

`m=(2*42)/12=color(red)(7 \ cm)`


`sinalpha=7/(7,3)`

`sinalpha=0,9589`

`color(red)(alpha=73,51°)`


`c=sqrt(12^2+7,3^2-2*12*7,3*cos73,51°)=color(red)(12,15 \ cm)`



5. Feladat
`i_("körív")=(r*pi*alpha)/(180°)=(6*pi*70°)/(180°)=color(red)(7,33 \ cm)`

`T_("körszelet")=(i*r)/2-(r^2*sinalpha)/2=(7,33*6)/2-(6^2*sin70°)/2=color(red)(5,08 \ cm^2)`