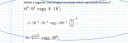Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Hatványozás
faragocsilla75
kérdése
157
Melyik a nagyobb? Számológépet nem lehet használni. Számolással kell megoldani.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1
kazah
megoldása
`6^9*9^3` = `2^9*3^9*3^(2*3)` = `2^9*3^(15)`
`8*18^7` = `2^3*2^7*3^(14)` = `2^(10)*3^(14)`
A kettő hányadosa: `(2^9*3^(15))/(2^(10)*3^(14))` = `2^(-1)*3` = `3/2` egynél nagyobb, így az első a nagyobb.
e,
`20^(-5)*16^(-8)` = `2^(-10)*5^(-5)*2^(4*(-8))` = `2^(-10-32)*5^(-5)`
`100^(-7)*(8/5)^(-9)` = `5^(2*(-7))*2^(2*-7)*2^(3*(-9))/5^(-9)` = `5^(-14-(-9))*2^(-14-27)` = `5^(-5)*2^(-41)`
`(2^(-42)*5^(-10))/(2^(-41)*5^(-5))` = `2^(-42-(-41))*5^(-10-(-5))` = `2^(-1)*5^(0) lt 1`, a második a nagyobb.
b,
`root(3)(7^(53))` = `7^(53/3)`
`49^9` = `7^(18)` = `7^(54/3)`
A második a nagyobb.
`8*18^7` = `2^3*2^7*3^(14)` = `2^(10)*3^(14)`
A kettő hányadosa: `(2^9*3^(15))/(2^(10)*3^(14))` = `2^(-1)*3` = `3/2` egynél nagyobb, így az első a nagyobb.
e,
`20^(-5)*16^(-8)` = `2^(-10)*5^(-5)*2^(4*(-8))` = `2^(-10-32)*5^(-5)`
`100^(-7)*(8/5)^(-9)` = `5^(2*(-7))*2^(2*-7)*2^(3*(-9))/5^(-9)` = `5^(-14-(-9))*2^(-14-27)` = `5^(-5)*2^(-41)`
`(2^(-42)*5^(-10))/(2^(-41)*5^(-5))` = `2^(-42-(-41))*5^(-10-(-5))` = `2^(-1)*5^(0) lt 1`, a második a nagyobb.
b,
`root(3)(7^(53))` = `7^(53/3)`
`49^9` = `7^(18)` = `7^(54/3)`
A második a nagyobb.
Módosítva: 1 éve
0
- Még nem érkezett komment!