1. feladat
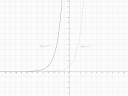
Itt nem tudom mennyire pontosan kell ábrázolni. Alapból az `e^x` egy exponenciális fv, vagyis kicsi `x`-ekre nagyon kicsi pozitív szám az értéke, `x=0`-nál 1 a fv érték és utána pedig minél nagyobb az `x`, annál nagyobb a fv érték. Ezzel szemben az `e^(x+4)` a függvénytranszformációknál tanultak miatt tudjuk, hogy balra van el tolva 4 egységgel. Ami azt jelenti, hogy ugyanolyan lesz a fv képe, mint az `e^x`-nek, csak ez `x=-4`-nél lesz 1 és utána kezd el nőni. Ennyi szerintem elég az ábrázoláshoz. (1-es ábra)

`y = e^(x+4)`
Az inverzhez megfordítjuk `x`-et és `y`-t és kifejezzük újra `y`-t:
`x = e^(y+4) " /"\ ln()`

`ln x = y+4 " /"-4`

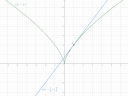
`y = ln x-4`

Ez pedig `ln x` eltolva 4-gyel lefelé. Ez egy logaritmus fv, úgyhogy tudjuk róla, hogy az exponenciális fv tükörképe az `y=x` tengelyre, vagyis csak `x=0`-tól értelmezett, ott `-oo`, majd 1-nél nulla a fv és utána szépen lassan tart a `oo`-be. (2-es ábra)

2. feladat
`f(x) = x^2+x", " g(x) = 1+x`

Csak be kell helyettesíteni az `f`-ben az `x` helyére a `g`-t.
`h(x) = (f @ g)(x) = (x+1)^2+(x+1) = x^2+2x+1+x+1 = x^2+3x+2`

Az ábrázoláshoz mondjuk alakítsuk teljes négyzetté:
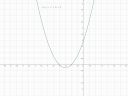
`h(x) = (x+3/2)^2-(3/2)^2+2 = (x+3/2)^2-1/4`

A másodfokú polinomról tudjuk, hogy U alakú a fv képe. Mivel pozitív a négyzetes tag, ezért felfelé néz az U, illetve a teljes négyzetes alakból látszik, hogy `3/2`-del van balra eltolva és `1/4`-del lefelé az origóhoz képest. (3-as ábra)

3. feladat
A derivált függvény adja meg a fv minden adott pontjában az érintőt egyenes meredekségét, vagyis a derivált fv kell az adott helyettesítési értékkel, illetve az, hogy áthaladjon egy adott ponton ez az egyenes:
`f'(x) = 2*2/3*x^(-1//3) = 4/3 x^(-1//3)`

`f'(a) = 4/3*1^(-1//3) = 4/3`

A pont pedig, amin rajta kell lennie az érintőnek az a fv `P(a; f(a))` pontja.
`f(a) = 2*1^(2//3) = 2`

Vagyis `m = 4/3", " P(1; 2)`, tehát az egyenes egyenlete:
`y-2 = 4/3 (x-1)`

`y = 4/3 x-4/3+2`

`y = 4/3 x+2/3` (4-es ábra)

4. feladat
Ahhoz, hogy a L'Hospital szabályt használhassuk, `0/0` alakú kell legyen a derivált (6-os ábra). Ha behelyettesítünk ez teljesül is, úgyhogy jók vagyunk. (több feltétele is van, de azok itt teljesülnek) Itt csak annyit kell tenni, hogy a számlálót és a nevezőt külön-külön kell deriválni és ezeknek a hányadosának a határértéke ugyanaz lesz, mint a határérték, amit keresünk: (illetve ezt többször is használhatjuk, amíg a feltételek teljesülnek)
`lim_(x->2) obrace(x^3-4x^2+4x)^0/ubrace(x^3-3x^2+4)_0 overset(L'H)(=) lim_(x->2) (d/(dx)(x^3-4x^2+4x))/(d/(dx)(x^3-3x^2+4)) ``=`` lim_(x->2) obrace(3x^2-8x+4)^0/ubrace(3x^2-6x)_0 overset(L'H)(=) lim_(x->2) (d/(dx)(3x^2-8x+4))/(d/(dx)(3x^2-6x)) ``=`` lim_(x->2) (6x-8)/(6x-6) = (6*2-8)/(6*2-6) = 4/6 = 2/3`

5. feladat
`f(x) = e^(-x^2)+(1+x^2)/ln x`

Itt csak az alap deriváltakat kell tudni, meg az alapvetőbb deriválási szabályokat. Csatolok róla képet. (5-ös ábra)
`f'(x) = e^(-x^2)*(-2x)+(2x*ln x-(1+x^2)*1/x)/ln^2 x = (2x)/ln x-(1+x^2)/(x ln^2 x)-2xe^(-x^2)`

6. feladat
`f(x) = x^3e^x`

Ma is tanultam valamit. Szóval az elaszticitás egy másik szó a konvexitásra. Zseniális. Sosem hallottam még szerintem. Mindenesetre egy konvexitás vizsgálattól nem riadok vissza! Először is kétszer le kell deriválni a függvényünket.
`f'(x) = 3x^2e^x+x^3e^x = (x^3+3x^2)e^x`

`f''(x) = (3x^2+6x)e^x+(x^3+3x^2)e^x = (x^3+6x^2+6x)e^x`

Majd pedig megnézzük, hogy hol nulla, mert ahol nulla, ott előjelet vált a második derivált fv értéke, vagyis megváltozik a konvexitás. Ha pedig nincs zérushelye, akkor végig vagy konvex, vagy konkáv a fv, attól függően, hogy pozitív-e a második derivált értéke, vagy sem.
`(x^3+6x^2+6x)e^x = 0`

`e^x` sosem nulla, úgyhogy csak akkor lesz ez nulla, ha a másik tag nulla:
`x^3+6x^2+6x = 0`
`x(x^2+6x+6) = 0`
`"I. " x_1 = 0`
`"II. "x^2+6x+6 = 0 => x_(2,3) = -3+-sqrt 3`

`{:(, {:]-oo; -3-sqrt 3[:}, -3-sqrt 3, {:]-3-sqrt 3; -3+sqrt 3[:}, -3+sqrt 3, {:]-3+sqrt 3; 0[:}, 0, {:]0; oo[:}),
(f''(x), -, "inf. p.", +, "inf. p.", -, "inf. p.", +),
(f(x), ◠\ "konkáv", -"0,933", ◡\ "konvex", -"0,574", ◠\ "konkáv", 0, ◡\ "konvex"):}`

7. feladat
`f(x) = 2x^3-6x+7`

Ez hasonló lesz, mint az előző feladat, csak itt az első deriváltat kell vizsgálni:
`f'(x) = 6x^2-6`

Ahol ez nulla, ott lokális minimum vagy maximum van, ahol negatív ott csökken a fv, ahol pozitív pedig növekszik.
`6x^2-6 = 0`
`6x^2 = 6`
`x^2 = 1`
`x = +-1`

`{:(, {:]-oo; -1[:}, -1, {:]-1; 1[:}, 1, {:]1; oo[:}),
(f'(x), +, "lok. max.", -, "lok. min.", +),
(f(x), "szig. mon. növ.", 11, "szig. mon. csökk.", 3, "szig. mon. növ."):}`

Ééés, ennyi volna... Nyugodtan szólj ha bármi nem világos!