Bármilyen logaritmusra:
`log_a x = 0 " /"a^(())`
`x = a^0 = 1`

`log_a x = 1 " /"a^(())`
`x = a^1 = a`

Vagyis bármilyen alapvető logaritmus fv-re, ahol 0 a fv érték ott a logaritmus argumentumának az értéke 1, és ahol 1 a fv érték ott a logaritmus argumentuma egyenlő a logaritmus alapjával. Illetve 0-ból jön a fv a `-oo`-ből. Viszont a logaritmus fv megjelenhet tükrözve és eltoltan is különböző előjelekkel és argumentumokkal. De mindegyikre, hogy bárhonnan is jön `+-oo`-ből a fv, eggyel odébb kellene 0-nak lennie az értékének, amiből következtethetünk az eltolásra. Azért ezek vannak bejelölve az ábrákon.

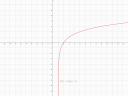
Tehát alapból egy logaritmus fv úgy néz ki, hogy 0-tól jön a `-oo`-ből. Vagyis a legelső eggyel el van tolva jobbra. A fv transzformációknál tanultak szerint ez azt jelenti a fv-ben, hogy `x` helyére `(x-a)`-t kell írni, ahol az `a` az eltolás előjeles mértéke. Itt `+1` az eltolás, mert a pozitív `x` tengely irányába van eltolva a fv, vagyis `(x-1)` lesz a logaritmus argumentuma. Illetve láthatjuk, hogy 3-nál 1 a fv érték, ami 2 lenne, ha nem volna eltolva a fv, hiszen 1-nél kéne 0-nak lennie a fv-nek, de 2-nél nulla az eltolás miatt, vagyis az alapunk 2 lesz:
`f(x) = log_2 (x-1)`

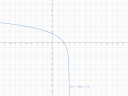
A másodiknál kicsit fura a helyzet, mert nem jobbra nő a fv, hanem balra, vagyis mintha tükrözve lenne az egész. Ez az `x` értékekre mit jelent? A jobboldal és a bal oldal fel van cserélve, de milyen `x`-ek vannak jobboldalt és milyenek vannak baloldalt? Pozitívok és negatívok. Vagyis ha `x` helyett `-x` van a logaritmuson belül, akkor azzal megfordul az egész fv. De akkor még a szaggatott vonal az `y` tengelyen lenne, ami még nem jó nekünk. Ez a fv is el van tolva vízszintesen, viszont ez most 3-mal és mivel az `x` negatív, itt fordított irányú lesz az eltolás is, vagyis nem +3, hanem -3 irányú, amiből `-(x-3)=(-x+3)` lesz a logaritmus belsejében. Az alapunk pedig továbbra is 2, mert megint 1 egységre van a zérushelytől az 1 fv értékű `x`, vagyis:
`g(x) = log_2 (-x+3)`

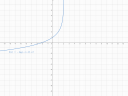
A harmadiknál láthatjuk, hogy itt nem `-oo`-ből jön a fv és balra nő, mint az előbb, hanem `+oo`-ből. Eről megint csak egy negatív előjel tehet, de ezúttal nem a logaritmuson belül, hanem az egész fv lesz negatív, vagyis valami ilyesmi lesz majd a végeredmény: `h(x) = -(log ...)`. Illetve itt ugyanúgy, mint az előbb nem jobbra tart a fv, hanem balra, tehát itt ugyanúgy, mint az előbb, a logaritmuson belül is negatív lesz az `x`. Továbbá a szaggatott vonal nem 0-nál van, hanem 2-nél, vagyis jobbra +2-vel el van tolva a fv, ami a `-x` miatt megfordul. Valamint, itt most a szaggatott vonaltól (x=2) 1 egységre (x=1) nem 0 a fv érték, vagyis nem metszi az `x` tengelyt, hanem itt az értéke 2, ami egy felfelé eltolást jelent. Eddig még ez nem volt. Ez a fv transzformációknál tanultaknál azt jelenti, hogy az egész fv-hez hozzá van adva valamilyen szám, valahogy így: `h(x) = (...)+b`, ahol a `b` a függőleges eltolás előjeles mértéke. Jelen esetben ez `+2`, mert az `y` tengely pozitív irányába történt az eltolás. Illetve megint csak 2-es alapú logaritmusunk van, mert ha visszatoljuk a fv függőlegesen, hogy 1-nél 0 legyen, akkor 0-nál -1 lesz, ami ugyanúgy 1 egységre van attól, ahol alapból 0 a logaritmus, vagyis ugyanarról a logaritmusról van szó, mint eddig. Tehát:
`h(x) = -log_2 (-x+2)+2`

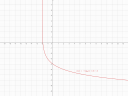
A negyedikhez ezek után pedig már mindent is tudunk úgy gondolom... Ez olyan, mint a legelső, vagyis ez jobbra tart, ahogy kell neki, vagyis ez nem lesz `-x`-es. Viszont nem nő, hanem csökken a fv, úgyhogy kívül lesz egy mínusz jel. Ez most nem pozitív irányba van vízszintesen eltolva, hanem negatív irányba 2-vel, úgyhogy most először `(x-(-2))=(x+2)` pozitív előjelű lesz `x` után a szám. Utána a szaggatott vonaltól 1 egységre kéne 0-nak lennie a fv-nek, de -3, vagyis -3-mal van eltolva függőlegesen, vagyis -3-at kell majd hozzáadni a logaritmus után. Illetve, noha nem jelölik, de szerintem -4-nél metszi az `y` tengelyt, vagyis ha visszacsinálunk minden transzformációt, az azt jelenti, hogy itt is 2-nél 1 a fv érték, vagyis 2-es alapú a logaritmusunk. Vagyis
`i(x) = -log_2 (x+2)-3`