Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Három erő egyensúlya
 dani-tolnai6947
kérdése
dani-tolnai6947
kérdése
593
Mechanika de szerintem matematikával is kapcsolatos.
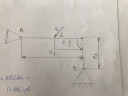
Alfa:45 fok
l1=3 méter
l2=1 méter
F=1000 Newton
1cm feleljen meg 250 Newtonnak
1cm feleljen meg 0,5 méternek
Mekkora az A csuklóban és a B rúdban fellépő erő nagysága?
Nem tudom hogy ebből az adatókból hogyan tudom kiszámolni. Ebben szeretnék segítséget kérni. Valamint meg is kell szerkeszteni és ezt sem tudom. Valaki legyen szives magyarázza el.
A végén ki kell rajzolni a párhuzamosokkal az erővonalakat úgy hogy 3 szöget hozzanak ki.
Előre is köszönöm.
Alfa:45 fok
l1=3 méter
l2=1 méter
F=1000 Newton
1cm feleljen meg 250 Newtonnak
1cm feleljen meg 0,5 méternek
Mekkora az A csuklóban és a B rúdban fellépő erő nagysága?
Nem tudom hogy ebből az adatókból hogyan tudom kiszámolni. Ebben szeretnék segítséget kérni. Valamint meg is kell szerkeszteni és ezt sem tudom. Valaki legyen szives magyarázza el.
A végén ki kell rajzolni a párhuzamosokkal az erővonalakat úgy hogy 3 szöget hozzanak ki.
Előre is köszönöm.
Jelenleg 1 felhasználó nézi ezt a kérdést.
mechanika, Matematika, erő, Egyensúlya
mechanika, Matematika, erő, Egyensúlya
0
Középiskola / Matematika
Válaszok
1 bongolo
{
bongolo
{  }
megoldása
}
megoldása
Az F erőt fel kell bontani két komponensre: egy függőlegesre (`F_y`) és egy vízszintesre (`F_x`). Ebből lesz a háromszög, amit meg kell rajzolnod. (Az F tetejétől húzz függőlegeset lefelé, az lesz az `F_y`, a csúcsából meg vízszinteset jobbra, az az `F_x`, de az balra mutat!)
A 45° miatt mindkettő azonos hosszú lesz:
`F_x = F/sqrt 2`
`F_y = F/sqrt 2`
Számold ki őket.
Az `F_y` ahogy felrajzoltad az `ℓ_1` rúd közepétől kicsit jobbra van, de ez nem igaz, valójában pont középen, az F nyilának a hegyénél hat. Ez a rajzon nem látszik, de tudni kell.
Na most az `ℓ_1` rúdra vízszintesen hat az `F_x` erő, kell egy ugyanakkora nagyságú de ellentétes irányú erőnek hatnia az A pontban is a rúdra ahhoz, hogy nulla legyen az eredőjük. Rajzolj oda egy olyan erőt, nevezd el mondjuk `F_1`-nek. Írd is fel, hogy mekkora az `F_1`. (Nem ez lesz a teljes erő, ami az A pontban hat, ez csak a vízszintes komponense lesz.)
Az `F_x` erő hatásvonala pont az A csuklón megy át, ezért annak nincs forgatónyomatéka az A-ra. Csak az `F_y`-nak van forgatónyomatéka.
A B rúdon a rúd irányában szabad hasson erő (más irányban nem hathat, mert akkor elforgatná). Az `ℓ_1` rúdra ebből a jobb oldali csuklón felfelé irányuló `F_B` erő fog hatni. Az A csuklóra számolva a forgatónyomatékok összege nulla kell legyen, mert nem mozdul el a rúd. Az `F_B` ellentétes irányú, mint `F_y`, ezért az előtt negatív előjel lesz:
`F_y·ℓ_1/2 - F_B·ℓ = 0`
Ami azt jelenti, hogy
`F_B = F_y/2`
(hisz lehetett `ℓ`-lel egyszerűsíteni)
Ezt számold is ki és rajzold fel az `ℓ_1` rúd jobb szélére felfelé.
Az `ℓ_1` rúdra ható függőleges irányú erőknek (erő-komponenseknek) az összege még nem nulla, tehát kell még lennie egy további erő-komponensnek is, hogy az eredő nulla legyen. (Azért tudjuk, hogy az eredő nulla, mert nem mozdul el a rúd.) Ez az erő az A pontban hat felfelé, nagysága pedig pont annyi, amennyi ahhoz kell, hogy az eredő 0 legyen. Nevezzük `F_2`-nek.
`F_2 + F_B= F_y`
Ez éppen `F_y/2`, ugye látod? Rajzold ezt is az ábrába az A csuklónál felfelé.
Az `F_1` és `F_2` erők eredője lesz az az `F_A` erő, ami az A pontban hat a rúdra. Szerkeszd meg a háromszöggel, két befogója `F_1` és `F_2`, az átfogója lesz `F_A`. Vigyázz, hogy milyen az iránya! Az `F_1` nyíl csúcsához húzzad felfelé az `F_2` hosszú befogót, úgy jön ki a háromszög az `F_A` átfogóval. Vagyis az `F_A` jobb-felfelé fog mutatni.
A hosszát elvileg le tudod olvasni a rajzról, ha pontosan szerkesztetted, de kijön pitagorasszal:
`F_A^2 = F_1^2+F_2^2`
`F_A = sqrt(F_1^2+F_2^2)`
A 45° miatt mindkettő azonos hosszú lesz:
`F_x = F/sqrt 2`
`F_y = F/sqrt 2`
Számold ki őket.
Az `F_y` ahogy felrajzoltad az `ℓ_1` rúd közepétől kicsit jobbra van, de ez nem igaz, valójában pont középen, az F nyilának a hegyénél hat. Ez a rajzon nem látszik, de tudni kell.
Na most az `ℓ_1` rúdra vízszintesen hat az `F_x` erő, kell egy ugyanakkora nagyságú de ellentétes irányú erőnek hatnia az A pontban is a rúdra ahhoz, hogy nulla legyen az eredőjük. Rajzolj oda egy olyan erőt, nevezd el mondjuk `F_1`-nek. Írd is fel, hogy mekkora az `F_1`. (Nem ez lesz a teljes erő, ami az A pontban hat, ez csak a vízszintes komponense lesz.)
Az `F_x` erő hatásvonala pont az A csuklón megy át, ezért annak nincs forgatónyomatéka az A-ra. Csak az `F_y`-nak van forgatónyomatéka.
A B rúdon a rúd irányában szabad hasson erő (más irányban nem hathat, mert akkor elforgatná). Az `ℓ_1` rúdra ebből a jobb oldali csuklón felfelé irányuló `F_B` erő fog hatni. Az A csuklóra számolva a forgatónyomatékok összege nulla kell legyen, mert nem mozdul el a rúd. Az `F_B` ellentétes irányú, mint `F_y`, ezért az előtt negatív előjel lesz:
`F_y·ℓ_1/2 - F_B·ℓ = 0`
Ami azt jelenti, hogy
`F_B = F_y/2`
(hisz lehetett `ℓ`-lel egyszerűsíteni)
Ezt számold is ki és rajzold fel az `ℓ_1` rúd jobb szélére felfelé.
Az `ℓ_1` rúdra ható függőleges irányú erőknek (erő-komponenseknek) az összege még nem nulla, tehát kell még lennie egy további erő-komponensnek is, hogy az eredő nulla legyen. (Azért tudjuk, hogy az eredő nulla, mert nem mozdul el a rúd.) Ez az erő az A pontban hat felfelé, nagysága pedig pont annyi, amennyi ahhoz kell, hogy az eredő 0 legyen. Nevezzük `F_2`-nek.
`F_2 + F_B= F_y`
Ez éppen `F_y/2`, ugye látod? Rajzold ezt is az ábrába az A csuklónál felfelé.
Az `F_1` és `F_2` erők eredője lesz az az `F_A` erő, ami az A pontban hat a rúdra. Szerkeszd meg a háromszöggel, két befogója `F_1` és `F_2`, az átfogója lesz `F_A`. Vigyázz, hogy milyen az iránya! Az `F_1` nyíl csúcsához húzzad felfelé az `F_2` hosszú befogót, úgy jön ki a háromszög az `F_A` átfogóval. Vagyis az `F_A` jobb-felfelé fog mutatni.
A hosszát elvileg le tudod olvasni a rajzról, ha pontosan szerkesztetted, de kijön pitagorasszal:
`F_A^2 = F_1^2+F_2^2`
`F_A = sqrt(F_1^2+F_2^2)`
Módosítva: 8 éve
0
- Még nem érkezett komment!