Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Soss
 Snnyhsd
kérdése
Snnyhsd
kérdése
457
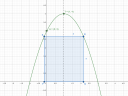
2. Az y = ax' + bx + c egyenletú parabola tengelypontja a T(1; 4) pont, a parabolára illeszkedik az A(0; 3) pont. Irjunk az x tengely által lemetszett parabolaszeletbe maximális területù téglalapot!
Adjuk meg a csúcsok koordinátáit!
Adjuk meg a csúcsok koordinátáit!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 Epyxoid
{ Tanár }
megoldása
Epyxoid
{ Tanár }
megoldása
Ha a parabola tengelypontja `T(1; 4)`, akkor a parabola egyenlete a `p` paraméter függvényében:
`(x-1)^2 = 2p(y-4)`
Illetve rajta kell lennie az `A` pontnak, vagyis
`(0-1)^2 = 2p(3-4)`
`1 = 2p*(-1)`
`-2p = 1`
`p = -1/2`
Vagyis a parabola egyenlete:
`(x-1)^2 = -(y-4)`
`x^2-2x+1 = 4-y`
`y = -x^2+2x+3`
Mivel a parabola szimmetrikus, így elég csak az egyik félre megkeresnünk a maximumot és a maximum a kétszerese lesz. Illetve az egész függvény el van tolva 1 egységgel jobbra az `y` tengelyhez képest, vagyis ha a "fél téglalap" egyik oldala `x`, akkor a másik oldalát úgy kapjuk, hogy ha eggyel nagyobb értéket helyettesítünk be, tehát:
`y = -(x+1)^2+2(x+1)+3 = -x^2 cancel(-2x)-1 cancel(+2x)+2+3 = -x^2+4`
A fél téglalap ennek a kettőnek a szorzata lesz:
`T(x) = x*(-x^2+4) = 4x-x^3`
`T'(x) = 4-3x^2`
`4-3x^2 = 0`
`3x^2 = 4`
`x = 2/sqrt(3) = (2 sqrt 3)/3`
`y = -((2 sqrt 3)/3)^2+4 = 4-(4*3)/9 = 4-4/3 = 8/3`
Vagyis egy `(4 sqrt 3)/3` és egy `8/3` oldalú téglalap területe lesz a maximális. A csúcsok koordinátái pedig úgy adódik, hogy az `x` koordináták `x=1`-től lesznek `+-(2 sqrt 3)/3` távolságra, az `y` koordináták pedig `0` és `8/3`, vagyis:
`P(1-(2 sqrt 3)/3; 0)", "Q(1+(2 sqrt 3)/3; 0)", "R(1+(2 sqrt 3)/3; 8/3)", "S(1-(2 sqrt 3)/3; 8/3)`
`(x-1)^2 = 2p(y-4)`
Illetve rajta kell lennie az `A` pontnak, vagyis
`(0-1)^2 = 2p(3-4)`
`1 = 2p*(-1)`
`-2p = 1`
`p = -1/2`
Vagyis a parabola egyenlete:
`(x-1)^2 = -(y-4)`
`x^2-2x+1 = 4-y`
`y = -x^2+2x+3`
Mivel a parabola szimmetrikus, így elég csak az egyik félre megkeresnünk a maximumot és a maximum a kétszerese lesz. Illetve az egész függvény el van tolva 1 egységgel jobbra az `y` tengelyhez képest, vagyis ha a "fél téglalap" egyik oldala `x`, akkor a másik oldalát úgy kapjuk, hogy ha eggyel nagyobb értéket helyettesítünk be, tehát:
`y = -(x+1)^2+2(x+1)+3 = -x^2 cancel(-2x)-1 cancel(+2x)+2+3 = -x^2+4`
A fél téglalap ennek a kettőnek a szorzata lesz:
`T(x) = x*(-x^2+4) = 4x-x^3`
`T'(x) = 4-3x^2`
`4-3x^2 = 0`
`3x^2 = 4`
`x = 2/sqrt(3) = (2 sqrt 3)/3`
`y = -((2 sqrt 3)/3)^2+4 = 4-(4*3)/9 = 4-4/3 = 8/3`
Vagyis egy `(4 sqrt 3)/3` és egy `8/3` oldalú téglalap területe lesz a maximális. A csúcsok koordinátái pedig úgy adódik, hogy az `x` koordináták `x=1`-től lesznek `+-(2 sqrt 3)/3` távolságra, az `y` koordináták pedig `0` és `8/3`, vagyis:
`P(1-(2 sqrt 3)/3; 0)", "Q(1+(2 sqrt 3)/3; 0)", "R(1+(2 sqrt 3)/3; 8/3)", "S(1-(2 sqrt 3)/3; 8/3)`
0
- Még nem érkezett komment!