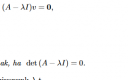Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Miért kerül ide a determináns? Saját-érték, sasját-vektor
 SharpMan
{ Elismert } kérdése
SharpMan
{ Elismert } kérdése
291
Levezetésnél bemutatták, hogy (A-lambda*I)v=0
Ugye akkor 0, ha v=0, a nullvektor mindennel párhuzamos vagy az első tag értéke 0.
Miért mégis ennek a determinánsát írja?
Remélem érethető mi a problémám.
Ugye akkor 0, ha v=0, a nullvektor mindennel párhuzamos vagy az első tag értéke 0.
Miért mégis ennek a determinánsát írja?
Remélem érethető mi a problémám.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
2 gyula205
válasza
gyula205
válasza
Úgy tűnik, hogy tévedésben vagy. Ugyanis az a bizonyos mátrixegyenlet nemcsak akkor lehet nulla, ha `v=0`. Nézd meg jobban, hogyan is szól a sajátérték és sajátvektor definíciója!
Az `A*v=lambdav` mátrixegyenlet nemtriviális megoldásait keressük. Vagyis `v ne 0`! Ez tömörebben úgy is felírható, hogy `(A-lambdaI)*v=0`. Nézz rá egy másik definíciócsoportra is, ami a karakterisztikus mátrixról és karakterisztikus polinomról szól továbbá arra a tételre is, ami a azt mondja ki, hogy (komplex) lineáris térben minden lineáris transzformációnak létezik legalább egy sajátvektora. Lényegében egy homogén lineáris egyenletrendszerhez jutunk és ez akkor és csak akkor szolgáltat triviálistól különböző megoldást, ha a szóban forgó determináns, azaz `det(A-lambdaI)=0`. Ez konkrétabban egy n-ed fokú polinomra felírt egyenlet és ennek a gyökei a sajátértékek. Remélem érthetően megválaszoltam a problémádhoz tartozó kérdést. ( Itt megjegyzem, hogy van egy másik tétel is, amely kimondja a karakterisztikus egyenlet gyökei függetlenek a bázis megválasztásától, de ez egy másik problémakörhöz kapcsolható).
Az `A*v=lambdav` mátrixegyenlet nemtriviális megoldásait keressük. Vagyis `v ne 0`! Ez tömörebben úgy is felírható, hogy `(A-lambdaI)*v=0`. Nézz rá egy másik definíciócsoportra is, ami a karakterisztikus mátrixról és karakterisztikus polinomról szól továbbá arra a tételre is, ami a azt mondja ki, hogy (komplex) lineáris térben minden lineáris transzformációnak létezik legalább egy sajátvektora. Lényegében egy homogén lineáris egyenletrendszerhez jutunk és ez akkor és csak akkor szolgáltat triviálistól különböző megoldást, ha a szóban forgó determináns, azaz `det(A-lambdaI)=0`. Ez konkrétabban egy n-ed fokú polinomra felírt egyenlet és ennek a gyökei a sajátértékek. Remélem érthetően megválaszoltam a problémádhoz tartozó kérdést. ( Itt megjegyzem, hogy van egy másik tétel is, amely kimondja a karakterisztikus egyenlet gyökei függetlenek a bázis megválasztásától, de ez egy másik problémakörhöz kapcsolható).
Módosítva: 3 éve
1
- Még nem érkezett komment!
 Epyxoid
{ Tanár }
válasza
Epyxoid
{ Tanár }
válasza
Annyi a lényeg, hogy `(A-lamda I)v = 0` ami csak akkor ad nullvektort, ha vagy a `v` nullvektor, viszont a sajátvektor definíció szerint nem lehet nullvektor. Vagy pedig az `(A-lamda I)` tagnak kell valahogyan egy nem nullvektort nullvektorrá tennie, ami csak akkor igaz, ha ennek a mátrixnak a determinánsa 0.
0
- Még nem érkezett komment!