Keresés


Toplista

Toplista
  • betöltés...

Magántanár kereső

Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!

Koszinusztétel

334
Egy antenna magasságának meghatározásához a síkságon egy egyenesen felvesszük rendre az A,B, és C pontokat, úgy, hogy AB = 60 m, BC = 30 m. A felvett pontokból az antenna rendre 40°,55°, illetve 70°-os szög alatt látszik. Milyen magas az antenna?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika

Válaszok

1
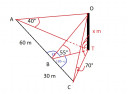
Én ezt inkább térben képzelem, bár lehet, hogy nem úgy van. (Ábra)

`bar(AT)=x/(tan40)` ; `bar(BT)=x/(tan50)` és `bar(CT)=x/(tan70)`

A koszinusztételt felírjuk az ABT háromszögre:

`(AB)^2=(AT)^2+(BT)^2-2*(AT)*(BT)*cosalpha`

Ugyanakkor a BCT-re is felírhatjuk:

`(BC)^2=(BT)^2+(CT)^2-2*(BT)*(CT)*cos(180-alpha)` = `(BT)^2+(CT)^2+2*(BT)*(CT)*cosalpha`

mert `cosalpha=-cos(180-alpha)`

I. `60^2=(x/(tan40))^2+(x/(tan55))^2-2*x/(tan40)*x/(tan55)*cosalpha`

II. `30^2=(x/(tan55))^2+(x/(tan70))^2+2*x/(tan55)*x/(tan70)*cosalpha`

I. `3600=x^2*(1.42+0.49-1.67*cosalpha)`

II. `900=x^2*(0.49+0.13+0.51*cosalpha)`

II.:I. :

`4=(1.91-1.67cosalpha)/(0.62+0.51*cosalpha)`

innen már menni fog szerintem

`cosalpha=-0.153`

I. `3600=x^2*(1.91-1.67*(-0.153))`

x = 40,77 m magas az antenna.

(Az elszámolás kockázatával)

Arról nincs szó, hogy az antenna az ABC egyenesen van.
Válasz kép
1