Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Szinusz és koszinusztétel
 Törölt
kérdése
Törölt
kérdése
417
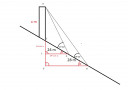
Milyen magas az az épület, amely a lábától egyenletesen lejtő úton mért 24 m távolásgból 35°50', és a lejgtőn 28 m-rel lejjebről 19°30'-es szög alatt látszik. Mekkora a lejtő hajlásszöge?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 kazah
megoldása
kazah
megoldása
Az ABO háromszögben az A csúcsnál levő szög:
180-35.83 = 144.17° ; az O csúcsnál pedig `180-(144.17+19.5)` = 16,33°
Szinusztétellel ki tudjuk számolni a AO szakasz hosszát:
`(AB)/(AO)=(sin O)/(sin B)`
`bar(AO)` = `((AB)*sinB)/(sinO)` = `(28*sin19.5)/(sin16.33)` = 33,235 m
Innen már az épület magasságát tudjuk számolni koszinusztétellel:
`bar(OE)=root()((AE)^2+(AO)^2-2*(AE)*(AO)*cos35.83)` = `root()(24^2+33.235^2-2*24*33.235*cos35.83)` = 19,68 m
Lejtő hajlásszöge:
Az ACE derékszögű háromszögben
`bar(AC)=24*sinalpha` és `bar(CE)=24*cosalpha`
ACO háromszögre felírjuk a Pitagorasz-tételt:
`(AC)^2+(AO)^2=(AO)^2`
`(19.68+24*sinalpha)^2+(24*cosalpha)^2=33.235^2`
`387.25+2*19.68*24*sinalpha+576*(sin^2alpha+cos^2alpha)=1104.565`
`944.64*sinalpha=141,315`
`sinalpha=0.1496`
`alpha=8,6°`.
180-35.83 = 144.17° ; az O csúcsnál pedig `180-(144.17+19.5)` = 16,33°
Szinusztétellel ki tudjuk számolni a AO szakasz hosszát:
`(AB)/(AO)=(sin O)/(sin B)`
`bar(AO)` = `((AB)*sinB)/(sinO)` = `(28*sin19.5)/(sin16.33)` = 33,235 m
Innen már az épület magasságát tudjuk számolni koszinusztétellel:
`bar(OE)=root()((AE)^2+(AO)^2-2*(AE)*(AO)*cos35.83)` = `root()(24^2+33.235^2-2*24*33.235*cos35.83)` = 19,68 m
Lejtő hajlásszöge:
Az ACE derékszögű háromszögben
`bar(AC)=24*sinalpha` és `bar(CE)=24*cosalpha`
ACO háromszögre felírjuk a Pitagorasz-tételt:
`(AC)^2+(AO)^2=(AO)^2`
`(19.68+24*sinalpha)^2+(24*cosalpha)^2=33.235^2`
`387.25+2*19.68*24*sinalpha+576*(sin^2alpha+cos^2alpha)=1104.565`
`944.64*sinalpha=141,315`
`sinalpha=0.1496`
`alpha=8,6°`.
1
- Még nem érkezett komment!