26
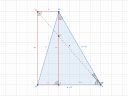
Elneveztem jó pár dolgot a feladatban. Az ábrán látszik, hogy mit, mire.
`b = MP = "8 cm, " a = PN = "6 cm, " alpha = hat(MPN) = 60°`

a)
Mivel `MAP` egy derékszögű háromszög, ami tartalmazza az `alpha` szöget, ezért felírhatjuk rá ennek a szinuszát és koszinuszát.
`sin alpha = m/b => m = b sin alpha = 8 sin 60° = 4 sqrt 3 ~~ "6,928 cm"`

`cos alpha = (a-n)/b => n = a-b cos alpha = 6-8 cos 60° = 6-4 = "2 cm"`

Vagyis `AMBN` kerülete:
`K = 2(m+n) = 2(4 sqrt 3+2) = 4+8 sqrt 3 ~~ "17,856 cm"`

b)
A `BPM` háromszögben ismerünk 2 oldalt, `n`-t és `b`-t, viszont egy szöget sem, de ezen könnyen segíthetünk. Ebben a háromszögben az `M` csúcsnál lévő szög két szögből áll: egy derékszögből és `beta`-ból. `beta` pedig az `MAP` háromszög másik szöge az `alpha` mellett, vagyis az értéke
`90+alpha+beta = 180 => beta = 90-alpha = 30°`

Tehát a `BPM` háromszögben az `M` csúcsnál lévő szög
`hat(BMP) = 90°+beta = 90+30 = 120°`

A `BP` átló hosszát pedig úgy kaphatjuk meg, hogy a `BNP` háromszöget nézzük. Ez egy derékszögű háromszög, aminek tudjuk két oldalát is, vagyis
`a^2+m^2=e^2 => e = sqrt(a^2+m^2) = sqrt(6^2+(4 sqrt 3)^2) = sqrt(36+48) = 2 sqrt 21 ~~ "9,165 cm"`

Így most már van két ismert oldalunk és velük szemben egy ismert és egy ismeretlen szögünk a háromszögben, vagyis felírhatunk egy szinusztételt a `BPM` háromszögre.
`sin varphi/(sin 120°) = n/e => sin varphi = (n sin 120°)/e = (2*sqrt(3)/2)/(2 sqrt 21) = 1/(2 sqrt 7) ~~ "0,189"`

c)
Mivel az `APQ` és az `MBQ` derékszögűek és a két háromszögnek a `Q` csúcsnál lévő szögeik csúcsszögek, vagyis ugyanakkorák, ezért a két háromszög hasonló, vagyis a megfelelő oldalaik aránya állandó. Ami a következőt jelenti:
`(AQ)/(QM) = (AP)/(BM) = (a-n)/n = (6-2)/2 = 4/2 = 2`

27.
a)
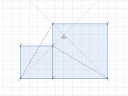
`ABF` és `MBC` két derékszögű háromszög, amiknek az egyik befogója az egyik négyzet oldala, a másik befogó pedig a másik négyzet oldala, vagyis a két háromszög egybevágó, vagyis az oldalaik megegyeznek egymással. Többek között
`AB = MB", " BF = BC`, így `AF = MC`

b)
`AM` és `FC` a két négyzet egy-egy átlója és mivel a két négyzet egyik oldala felfekszik ugyanarra az egyenesre, vagyis a két négyzet egyállású, ezért az átlóik vagy párhuzamosak, vagy pedig merőlegesek. Mivel ezeknek az átlóknak van metszéspontjuk, így párhuzamosak nem lehetnek, vagyis merőlegesek.

Az ábrán jól látszik: https://www.geogebra.org/calculator/c6yezyq2 (lehet mozgatni a `B` csúcsot! )

Elég szemét feladatok. Szólj ha bármi kérdésed van!