Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Konvex deltoid területe, szögei
 Bemmus
kérdése
Bemmus
kérdése
3014
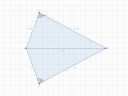
a, Egy konvex Deltoid két oldalának hossza 7 cm, illetve 14 cm, és ezek 82,2 °-os szöget zárnak be. Számítsd ki a deltoid területét!
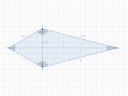
b, Egy konvex Deltoid két oldalának hossza 7 cm és 14 cm, és az egyik átló hossza is 7 cm. Számítsd ki a Deltoid szögeit, területét és a másik átló hosszát!
Neki kezdtem ennek a feladatnak, de nem tudom, hogy pontosan hogyan oldjam meg, valaki letudná vezetni nekem? előre is köszönöm a segítséget!
b, Egy konvex Deltoid két oldalának hossza 7 cm és 14 cm, és az egyik átló hossza is 7 cm. Számítsd ki a Deltoid szögeit, területét és a másik átló hosszát!
Neki kezdtem ennek a feladatnak, de nem tudom, hogy pontosan hogyan oldjam meg, valaki letudná vezetni nekem? előre is köszönöm a segítséget!
Jelenleg 1 felhasználó nézi ezt a kérdést.
11. osztály, Matematika, házi, deltoid
11. osztály, Matematika, házi, deltoid
0
Középiskola / Matematika
Válaszok
1 Epyxoid
{ Tanár }
megoldása
Epyxoid
{ Tanár }
megoldása
a) `a = "7 cm, " b = "14 cm, " beta = "82,2°"`
A deltoid szimmetrikus az egyik átlójára, vagyis olyan, mintha két ugyanolyan háromszögből állna. Mi ennek a háromszögnek ismerjük két oldalát és az ezek közti szöget. Ebből egyből számolható "fél deltoid háromszögnek" a területe, a deltoid területe pedig ennek a kétszerese lesz. Vagyis
`T_/_\\ = (ab sin beta)/2`
`T_"deltoid" = 2* T_/_\\ = ab sin beta = 7*14 sin "82,2°" ~~ "97,093 cm"^2`
Lehet ezt bonyolultabban is, de én nem látom értelmét. Ennyi adat bőven elég a területhez.
b) `a = "7 cm, " b = "14 cm, " e = "7 cm"`
Itt az a különbség, hogy nem tudjuk a két eltérő oldal közötti szöget, hanem helyette a rövidebbik átlót ismerjük. Kicsit szemét a feladat, hogy nem mondja meg, hogy ez a rövidebbik, de ez könnyen belátható, mert hogy ha a hosszabb lenne, akkor ez az átló és a deltoid két eltérő oldala egy háromszöget alkotna. Viszont a 7-7-14 oldalú háromszög az nem háromszög, mivel a két rövidebbik oldal nem hosszabb a leghosszabb oldalnál, vagyis ez egy vonal lenne egy háromszög helyett.
Ha viszont a rövidebbik átlóról van szó, akkor az a rövidebbik oldalakkal és a hosszabbik oldalakkal is két egyenlő szárú háromszöget alkot. Illetve a rövidebbik oldallal egyenlő oldalú háromszöget, mert a rövidebbik oldal ugyanolyan hosszú, mint ez az átló. Ha viszont egyenlő oldalú háromszöget alkot, annak minden szöge is egyenlő, vagyis egyből tudjuk, hogy a deltoid rövidebbik oldalai által bezárt szög `60°` fokot ad. Legyen ez az `alpha` szög. A `beta` az legyen itt is a két eltérő oldal közötti szög. Ebből van 2 ugyanakkora a szimmetria miatt. Az utolsó, hosszabbik oldalak által bezárt szög pedig legyen `gamma`.
A hosszabbik oldalak az átlóval pedig ahogy mondtam egyenlő szárú háromszöget alkotnak. Most nézzük ezt. Ahhoz, hogy megkapjuk a `gamma` szöget használhatnánk koszinusztételt is, de az nagy és otromba. Csinálhatjuk egyszerűbben is. Ha megfelezzük ezt az háromszöget a deltoid másik (egyelőre ismeretlen) átlója mentén, akkor derékszögű háromszögeket kapunk, aminek az egyik szöge `gamma"/2"`, a másikat `beta_1`-nek nevezem, az oldalai pedig a deltoid hosszabbik oldala, mint átfogó jelenik meg a háromszögben, az egyik befogó `e"/"2` , a rövidebb átló fele, a másik befogó pedig a deltoid másik átlójának egy része, de ez minket nem izgat. Ami minket érdekel az ez:
`sin(gamma"/"2) = (e"/"2)/b => gamma = 2 sin^"-1"((e"/"2)/b) = 2 sin^"-1"((7"/"2)/14) = 2 sin^"-1"(1/4) ~~ "28,955°"`
A másik 2 `beta_1` szög pedig úgy adódik, hogy a háromszög belső szögeinek összege 180°, vagyis
`gamma+2 beta_1 = 180° => beta_1 = (180-gamma)/2 ~~ "75,522°"`
Ezt azért nevezem `beta_1`-nek, mert a deltoid szimmetrikus `beta` szögének csak egy része. Az `e` átló kettébontja ezeket a `beta` szögeket. A másik felel a rövidebbik oldal és az átló által alkotott háromszögben van. Viszont mivel az tudjuk, hogy egyenlő oldalú, ezért a `beta_2 = 60°` lesz, vagyis
`beta = beta_1+beta_2 ~~ "135,522°"`
Tehát a deltoid szögei: `alpha = 60°", " beta = "135,522°, " gamma = "28,955°"`
A területet megint csak nem spiláznám túl. Ugyanúgy, mint előbb:
`T = ab sin beta = 7*14 sin "135,522°" ~~ "68,662 cm"^2`
A másik átlót pedig számolhatjuk a koszinusztétellel akár
`(f^2 = a^2+b^2-2ab cos beta)`
De számolhatjuk a terület képletből is! Miért is ne! Abban nincs annyi négyzet, meg gyök. A deltoid másik terület képlete:
Abban nincs annyi négyzet, meg gyök. A deltoid másik terület képlete:
`T = (ef)/2` (ahol `e` és `f` az átlók, nem az oldalak!!)
Ezt egyenlővé tehetjük a másikkal és kifejezhetjük belőle `f`-et.
`(ef)/2 = ab sin beta => f = (2ab sin beta)/e = (2*7*14 sin beta)/7 = 28 sin beta ~~ "19,618 cm"`
Bármi kérdésed van, nyugodtan kérdezz!
A deltoid szimmetrikus az egyik átlójára, vagyis olyan, mintha két ugyanolyan háromszögből állna. Mi ennek a háromszögnek ismerjük két oldalát és az ezek közti szöget. Ebből egyből számolható "fél deltoid háromszögnek" a területe, a deltoid területe pedig ennek a kétszerese lesz. Vagyis
`T_/_\\ = (ab sin beta)/2`
`T_"deltoid" = 2* T_/_\\ = ab sin beta = 7*14 sin "82,2°" ~~ "97,093 cm"^2`
Lehet ezt bonyolultabban is, de én nem látom értelmét. Ennyi adat bőven elég a területhez.

b) `a = "7 cm, " b = "14 cm, " e = "7 cm"`
Itt az a különbség, hogy nem tudjuk a két eltérő oldal közötti szöget, hanem helyette a rövidebbik átlót ismerjük. Kicsit szemét a feladat, hogy nem mondja meg, hogy ez a rövidebbik, de ez könnyen belátható, mert hogy ha a hosszabb lenne, akkor ez az átló és a deltoid két eltérő oldala egy háromszöget alkotna. Viszont a 7-7-14 oldalú háromszög az nem háromszög, mivel a két rövidebbik oldal nem hosszabb a leghosszabb oldalnál, vagyis ez egy vonal lenne egy háromszög helyett.
Ha viszont a rövidebbik átlóról van szó, akkor az a rövidebbik oldalakkal és a hosszabbik oldalakkal is két egyenlő szárú háromszöget alkot. Illetve a rövidebbik oldallal egyenlő oldalú háromszöget, mert a rövidebbik oldal ugyanolyan hosszú, mint ez az átló. Ha viszont egyenlő oldalú háromszöget alkot, annak minden szöge is egyenlő, vagyis egyből tudjuk, hogy a deltoid rövidebbik oldalai által bezárt szög `60°` fokot ad. Legyen ez az `alpha` szög. A `beta` az legyen itt is a két eltérő oldal közötti szög. Ebből van 2 ugyanakkora a szimmetria miatt. Az utolsó, hosszabbik oldalak által bezárt szög pedig legyen `gamma`.
A hosszabbik oldalak az átlóval pedig ahogy mondtam egyenlő szárú háromszöget alkotnak. Most nézzük ezt. Ahhoz, hogy megkapjuk a `gamma` szöget használhatnánk koszinusztételt is, de az nagy és otromba. Csinálhatjuk egyszerűbben is. Ha megfelezzük ezt az háromszöget a deltoid másik (egyelőre ismeretlen) átlója mentén, akkor derékszögű háromszögeket kapunk, aminek az egyik szöge `gamma"/2"`, a másikat `beta_1`-nek nevezem, az oldalai pedig a deltoid hosszabbik oldala, mint átfogó jelenik meg a háromszögben, az egyik befogó `e"/"2` , a rövidebb átló fele, a másik befogó pedig a deltoid másik átlójának egy része, de ez minket nem izgat. Ami minket érdekel az ez:
`sin(gamma"/"2) = (e"/"2)/b => gamma = 2 sin^"-1"((e"/"2)/b) = 2 sin^"-1"((7"/"2)/14) = 2 sin^"-1"(1/4) ~~ "28,955°"`
A másik 2 `beta_1` szög pedig úgy adódik, hogy a háromszög belső szögeinek összege 180°, vagyis
`gamma+2 beta_1 = 180° => beta_1 = (180-gamma)/2 ~~ "75,522°"`
Ezt azért nevezem `beta_1`-nek, mert a deltoid szimmetrikus `beta` szögének csak egy része. Az `e` átló kettébontja ezeket a `beta` szögeket. A másik felel a rövidebbik oldal és az átló által alkotott háromszögben van. Viszont mivel az tudjuk, hogy egyenlő oldalú, ezért a `beta_2 = 60°` lesz, vagyis
`beta = beta_1+beta_2 ~~ "135,522°"`
Tehát a deltoid szögei: `alpha = 60°", " beta = "135,522°, " gamma = "28,955°"`
A területet megint csak nem spiláznám túl. Ugyanúgy, mint előbb:
`T = ab sin beta = 7*14 sin "135,522°" ~~ "68,662 cm"^2`
A másik átlót pedig számolhatjuk a koszinusztétellel akár
`(f^2 = a^2+b^2-2ab cos beta)`
De számolhatjuk a terület képletből is! Miért is ne!
 Abban nincs annyi négyzet, meg gyök. A deltoid másik terület képlete:
Abban nincs annyi négyzet, meg gyök. A deltoid másik terület képlete:`T = (ef)/2` (ahol `e` és `f` az átlók, nem az oldalak!!)
Ezt egyenlővé tehetjük a másikkal és kifejezhetjük belőle `f`-et.
`(ef)/2 = ab sin beta => f = (2ab sin beta)/e = (2*7*14 sin beta)/7 = 28 sin beta ~~ "19,618 cm"`
Bármi kérdésed van, nyugodtan kérdezz!

Módosítva: 3 éve
-1
- Még nem érkezett komment!