Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matematika
 Törölt
kérdése
Törölt
kérdése
364
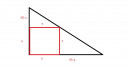
Mekkorák a 30 cm és 45 cm befogójú derékszögű háromszögbe írható maximális területű téglalap oldalai, ha a téglalap egyik szöge a háromszög derékszögével esik egybe?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
2 kazah
válasza
kazah
válasza
Hasonló háromszögek:
`y/(30-x)=45/30`
30y=45(30-x)
y=`45-3/2*x`
T = xy = `45x-3/2*x^2`
`T_("max") ` = `(dT)/(dx)` = 45-3*x =0
45 = `3*x`
x = 15
y = `45-3/2*15` = 22,5
T = xy = `15*22.5` = 337,5 `cm^2`
`y/(30-x)=45/30`
30y=45(30-x)
y=`45-3/2*x`
T = xy = `45x-3/2*x^2`
`T_("max") ` = `(dT)/(dx)` = 45-3*x =0
45 = `3*x`
x = 15
y = `45-3/2*15` = 22,5
T = xy = `15*22.5` = 337,5 `cm^2`
0
- Még nem érkezett komment!
 Epyxoid
{ Tanár }
megoldása
Epyxoid
{ Tanár }
megoldása
Oké. Ez egy jó kis deriválós feladat.
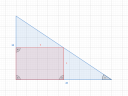
Én úgy képzelem el az egészet, hogy a 45-ös oldalán fekszik a háromszög és bal oldalt van a derékszög, jobb oldalt pedig az egyik hegyesszög, ami legyen `alpha`. Mivel a téglalap egyik szöge a háromszög derékszöge, ezért a téglalap két oldala felfekszik a háromszög befogóira. Nevezzük a téglalap függőleges oldalát `x`-nek, a vízszinteset pedig `y`-nak. `x` függvényében úgy kaphatjuk a téglalap másik oldalát, `y`-t, hogy észrevesszük, hogy az `x` oldal a háromszög `alpha` szögével egy derékszögű háromszöget alkot. Erre felírhatjuk `alpha` tangensét:
`"tg"\ alpha = x/(45-y)`
`45-y = x/("tg"\ alpha)`
`y = 45-x/("tg"\ alpha)`
Ezzel megvan a kapcsolat a téglalap két oldala között. Már csak `"tg"\ alpha` értékét kéne tudnunk, de az könnyen megkapható, hogy ha az eredeti derékszögű háromszögre írjuk fel:
`"tg"\ alpha = 30/45 = 2/3`
Ezt behelyettesítve a következőt kapjuk `y`-ra:
`y = 45-x/(2/3) = 45-3/2 x`
Ezek után minket a téglalap területe érdekel. Ez `x` függvényében a következő:
`T(x) = x*y = x*(45-(3x)/2) = 45x-3/2 x^2`
Ez egy függvénye `x`-nek, aminek akkor van szélsőértéke (minimuma, vagy maximuma), hogyha a derivált 0. Nézzük a deriváltat.
`T'(x) = 45-3x`
Mivel látjuk, hogy ez egy csökkenő függvény, az azt jelenti, hogy mielőtt nullává válna az értéke azelőtt pozitív a fv, utána pedig negatív, vagyis a zérushelye előtt nő a `T(x)` fv, utána pedig csökken, vagyis `T'(x)=0` valóban egy maximumhely lesz.
Most tegyük egyenlővé 0-val:
`45-3x = 0 " /"+3x`
`3x = 45 " /":3`
`x = 15`
`y = 45-(3*15)/2 = 45-45/2 = 45/2 = "22,5"`
Vagyis akkor lesz a beírható téglalap területe a legnagyobb, ha a téglalap a derékszög `"30 cm"`-es oldalával párhuzamos oldala `"15 cm"`, a `"45 cm"`-essel párhuzamos pedig `"22,5 cm"`, vagyis pont ezen befogóknak a felénél!
Én úgy képzelem el az egészet, hogy a 45-ös oldalán fekszik a háromszög és bal oldalt van a derékszög, jobb oldalt pedig az egyik hegyesszög, ami legyen `alpha`. Mivel a téglalap egyik szöge a háromszög derékszöge, ezért a téglalap két oldala felfekszik a háromszög befogóira. Nevezzük a téglalap függőleges oldalát `x`-nek, a vízszinteset pedig `y`-nak. `x` függvényében úgy kaphatjuk a téglalap másik oldalát, `y`-t, hogy észrevesszük, hogy az `x` oldal a háromszög `alpha` szögével egy derékszögű háromszöget alkot. Erre felírhatjuk `alpha` tangensét:
`"tg"\ alpha = x/(45-y)`
`45-y = x/("tg"\ alpha)`
`y = 45-x/("tg"\ alpha)`
Ezzel megvan a kapcsolat a téglalap két oldala között. Már csak `"tg"\ alpha` értékét kéne tudnunk, de az könnyen megkapható, hogy ha az eredeti derékszögű háromszögre írjuk fel:
`"tg"\ alpha = 30/45 = 2/3`
Ezt behelyettesítve a következőt kapjuk `y`-ra:
`y = 45-x/(2/3) = 45-3/2 x`
Ezek után minket a téglalap területe érdekel. Ez `x` függvényében a következő:
`T(x) = x*y = x*(45-(3x)/2) = 45x-3/2 x^2`
Ez egy függvénye `x`-nek, aminek akkor van szélsőértéke (minimuma, vagy maximuma), hogyha a derivált 0. Nézzük a deriváltat.
`T'(x) = 45-3x`
Mivel látjuk, hogy ez egy csökkenő függvény, az azt jelenti, hogy mielőtt nullává válna az értéke azelőtt pozitív a fv, utána pedig negatív, vagyis a zérushelye előtt nő a `T(x)` fv, utána pedig csökken, vagyis `T'(x)=0` valóban egy maximumhely lesz.
Most tegyük egyenlővé 0-val:
`45-3x = 0 " /"+3x`
`3x = 45 " /":3`
`x = 15`
`y = 45-(3*15)/2 = 45-45/2 = 45/2 = "22,5"`
Vagyis akkor lesz a beírható téglalap területe a legnagyobb, ha a téglalap a derékszög `"30 cm"`-es oldalával párhuzamos oldala `"15 cm"`, a `"45 cm"`-essel párhuzamos pedig `"22,5 cm"`, vagyis pont ezen befogóknak a felénél!
Módosítva: 3 éve
0
-
kazah: Hát igen, úgy látszik még a főiskolán is mesélni kell, nemcsak az óvodában
 Lehet, hogy nekem is kellett volna járnom egyetemre és akkor jókat tudtam volna aludni.
3 éve
1
Lehet, hogy nekem is kellett volna járnom egyetemre és akkor jókat tudtam volna aludni.
3 éve
1
-
Epyxoid: A matek iskolától függetlenül nem szokott menni általában az embereknek. Persze ha egyetemen nem megy az nagyobb gondot jelent, de általában valahogy mindig megoldják még így is az emberek. Mintha irónia szagát érezném...
 3 éve
0
3 éve
0
-
kazah: Igen, az volt
 3 éve
0
3 éve
0
-
Epyxoid: Milyen jó is volt sírva álomba szenderülni...
 A régi jó egyetemi évek. Nem tudod miről maradtál le!
A régi jó egyetemi évek. Nem tudod miről maradtál le!  3 éve
0
3 éve
0
-
kazah: Szerencsére nem tudom...csak látom a környezetemet és a tudatlanságot, ami körülvesz, továbbá amit itt látok, nekem már az is elég, hogy sírjak (vagy sírva röhögjek)
 3 éve
0
3 éve
0