Szerintem rajzzal ügyeskedni a legegyszerűbb. Én először beteszem úgy a számokat a halmazokba, ahogy a kifejezésekben vannak úgy, hogy belelógjanak azokba a tartományokba amiket érintenek, aztán belülről kifelé haladva kizárásos alapon felosztom a számokat addig, amíg mindegyik szám csak pontosan egy tartományon belül van.

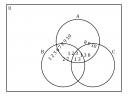
Például az 1-es ábrából úgy lehet elindulni, miután elhelyeztük a feladatban meghatározott számokat, hogy tudjuk, hogy az 1; 3 van csak mindhárom halmaz metszetében, vagyis az olyanok, mint az 1; 2; 3 felbonthatóak: az 1; 3 megy középre, a maradék 2-es pedig a másik tartományba amibe még belelógott. Ugyanúgy az 1; 3; 8-nál: mivel az 1; 3 van középen, ezért a 8-as a másik tartományban lesz amibe még benne volt. Aztán a 8; 9; 10 bontható fel és így tovább.

A 6-os szám elhelyezése kicsit trükkös volt, de mivel tudjuk, hogy `A nn B`-ben nincs benne, se az `A\ \\\ B`-ben, se a `B\ \\\ C`-ben, de tudjuk, hogy a `B`-ben van, ezért csak a `B` és `C` közös részébe kerülhet.

A maradék számok pedig a 4; 5 oda kerülhet csak, amelyik tartomány nem került szóba, vagyis a `C`-be, kizárásos alapon.

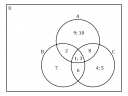
Na de az ábra alapján már látható a megoldás:
`A = {1; 2; 3; 8; 9; 10}`
`B = {1; 2; 3, 6; 7}`
`C = {1; 3; 4; 5; 6; 8}`

Nem egyszerű feladat. Gyakorolni kell. Nekem is meg kell vele birkózni, de kilogikázható.

Szólj nyugodtan ha bármi kérdésed lenne!