Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Halmazelmélet
 ムskpa5rik
kérdése
ムskpa5rik
kérdése
263
Ebben a szorgalmi feladtban kérném a segítségeteket, magyarázattal!
Köszönöm!
Köszönöm!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 Epyxoid
{ Tanár }
megoldása
Epyxoid
{ Tanár }
megoldása
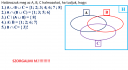
1. Az `A uu B uu C` mind a három halmaz összes elemét tartalmazza, így tudjuk, hogy ezt a 8 számjegy alkotja a 3 halmazt.
2. Ebből tudjuk, hogy ezek a számok mind benne vannak az `A` halmazban és a `B` és `C` közül valamelyikben, akár mindkettőben, ezt nem tudjuk. Tehát eddig, ami biztos, hogy `A = {1; 3; 5; 6}`, de ez még bővülhet.
3. Ebből azt tudjuk, hogy ez benne van a `C` halmazban, tehát eddig a `C = {8}`.
4. Ebből azt tudjuk, hogy ezek mind benne vannak az `A`-ban, vagyis bővítsük az eddigi halmazunkat: `A = {1; 2; 3; 5; 6; 7}`. Illetve azt is megtudtuk ebből, hogy ezek nincsenek benne a `B` halmazban, viszont a 2-esből tudjuk, hogy az 1, 3, 5, 6 az benne van vagy a `B`-ben, vagy a `C`-ben, viszont az 1, 2, 6, 7 most tudtuk meg, hogy biztosan nincs benne a `B`-ben, tehát az 1 és a 6 egyértelműen csak a `C`-ben lehet: `C = {1; 6; 8}`. A maradék 3 és 5 az pedig vagy a `B`-ben van, vagy mindkettőben. Még nem tudjuk.
5. Ebből pedig azt tudjuk meg, hogy a 3 a `B`-ben is és a `C`-ben is benne van, vagyis mindháromban! Vagyis `B = {3}", " C = {1; 3; 6; 8}`. Illetve azt eddig is tudtuk, hogy a 3 és az 5 vagy a `B`-ben, vagy a `C`-ben van, de most már tudjuk, hogy csak a 3-as van mindkettőben, vagyis az 5-ös nincs a `C`-ben, tehát a `B`-ben van: `B = {3; 5}`.
Valamint összesen 1 tartományt nem érintett egyik állítás sem az 5-ből: hogy mi van csak a `B`-ben. (Ez az 1-es ábrából jobban látszik. Ott úgy helyeztem el az egyes kijelentéseket, hogy azokba a tartományokba lógjanak bele, amelyiket érintik. Ebből látszik melyik rész nincs érintve.) Illetve van még egy szám, amiről szintén nem tesz egyik állítás sem kijelentést, ez a 4-es szám. Tehát a 4-es csakis a `B` halmazba kerülhet. `B = {3; 4; 5}`
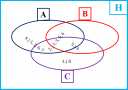
Ezzel a következőt kaptuk (2-es ábra):
`A = {1; 2; 3; 5; 6; 7}`
`B = {3; 4; 5}`
`C = {1; 3; 6; 8}`
Annak ellenőrzése pedig, hogy tényleg visszakapjuk-e az 5 állításban szereplőket az házi feladat!
2. Ebből tudjuk, hogy ezek a számok mind benne vannak az `A` halmazban és a `B` és `C` közül valamelyikben, akár mindkettőben, ezt nem tudjuk. Tehát eddig, ami biztos, hogy `A = {1; 3; 5; 6}`, de ez még bővülhet.
3. Ebből azt tudjuk, hogy ez benne van a `C` halmazban, tehát eddig a `C = {8}`.
4. Ebből azt tudjuk, hogy ezek mind benne vannak az `A`-ban, vagyis bővítsük az eddigi halmazunkat: `A = {1; 2; 3; 5; 6; 7}`. Illetve azt is megtudtuk ebből, hogy ezek nincsenek benne a `B` halmazban, viszont a 2-esből tudjuk, hogy az 1, 3, 5, 6 az benne van vagy a `B`-ben, vagy a `C`-ben, viszont az 1, 2, 6, 7 most tudtuk meg, hogy biztosan nincs benne a `B`-ben, tehát az 1 és a 6 egyértelműen csak a `C`-ben lehet: `C = {1; 6; 8}`. A maradék 3 és 5 az pedig vagy a `B`-ben van, vagy mindkettőben. Még nem tudjuk.
5. Ebből pedig azt tudjuk meg, hogy a 3 a `B`-ben is és a `C`-ben is benne van, vagyis mindháromban! Vagyis `B = {3}", " C = {1; 3; 6; 8}`. Illetve azt eddig is tudtuk, hogy a 3 és az 5 vagy a `B`-ben, vagy a `C`-ben van, de most már tudjuk, hogy csak a 3-as van mindkettőben, vagyis az 5-ös nincs a `C`-ben, tehát a `B`-ben van: `B = {3; 5}`.
Valamint összesen 1 tartományt nem érintett egyik állítás sem az 5-ből: hogy mi van csak a `B`-ben. (Ez az 1-es ábrából jobban látszik. Ott úgy helyeztem el az egyes kijelentéseket, hogy azokba a tartományokba lógjanak bele, amelyiket érintik. Ebből látszik melyik rész nincs érintve.) Illetve van még egy szám, amiről szintén nem tesz egyik állítás sem kijelentést, ez a 4-es szám. Tehát a 4-es csakis a `B` halmazba kerülhet. `B = {3; 4; 5}`
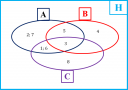
Ezzel a következőt kaptuk (2-es ábra):
`A = {1; 2; 3; 5; 6; 7}`
`B = {3; 4; 5}`
`C = {1; 3; 6; 8}`
Annak ellenőrzése pedig, hogy tényleg visszakapjuk-e az 5 állításban szereplőket az házi feladat!

Módosítva: 3 éve
0
- Még nem érkezett komment!