Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matek házi
 bartam34
{ Fortélyos } kérdése
bartam34
{ Fortélyos } kérdése
332
A megoldásokat köszönöm szépen, az utolsó feladatban megköszönnék egy kis(ebb) magyarázatot is!
A háromszöges feladathoz is jó lenne magyarázat! És ábra (grafikon) mindenekelőtt! KÖSZI!!!
A feladatok:
A háromszöges feladathoz is jó lenne magyarázat! És ábra (grafikon) mindenekelőtt! KÖSZI!!!
A feladatok:
Jelenleg 1 felhasználó nézi ezt a kérdést.
sos, matekházi, egyenletek, megoldás, háromszög, koordinátarendszer, matektanár, irányvektor, irányszög, normálvektor
sos, matekházi, egyenletek, megoldás, háromszög, koordinátarendszer, matektanár, irányvektor, irányszög, normálvektor
0
Középiskola / Matematika
Válaszok
2 Epyxoid
{ Tanár }
válasza
Epyxoid
{ Tanár }
válasza
1. Egy gond van: nem tudom mi szerint kéne jellemezni. De nézzük akkor nagy vonalakban... Csak ami az ábrázoláshoz kell.
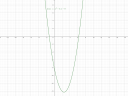
a) `f(x) = x^2-5x-8`
Ez egy parabola, vagyis egy másodfokú polinom, ami azt jelenti, hogy ha az `x^2`-es tag pozitív, akkor `uu` alakú a függvény képe, ha negatív, akkor pedig `nn` alakú. Itt pozitív, szóval van neki egy minimuma. Ha egy kicsit átalakítjuk a teljes négyzetes formájába akkor leolvasható róla a minimuma:
`x^2-5x-8 = (x-5/2)^2-25/4-8 = (x-5/2)^2-57/4`
A függvénytranszformációkat ismerve láthatjuk, hogy ez az eredeti `x^2` függvény eltolva jobbra `5/2`-del és lefele `57/4`-del, vagyis a `T(5/2"; " -57/4)` pontban van az U alak csúcsa és onnan ível szépen felfelé. Ami azt is jeleni, hogy `5/2`-ig csökken a függvény értéke és utána pedig nő.
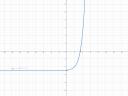
b) `g(x) = 3^(x-2)-5`
Ez egy exponenciális függvény, ami azt jelenti negatív számokra nagyon kicsi a fv értéke, viszont pozitív irányba nagyon hamar megugrik. Vagyis alapból a `3^x` balról a 0-ból jön, az `y` tengelyhez érve 1 az értéke, majd pedig szinte azonnal felfele kanyarodik és megy a `oo`-be. Ez a függvény viszont el van tolva jobbra 2-vel és lefele 5-tel. Vagyis ez -5-ből jön és majd csak `x=2`-nél lesz az értéke `1-5 = -4` (mivel -5-tel el van tolva) és utána ugyanúgy elhúz a végtelenbe. Illetve a fv az egész tartományán növekvő.
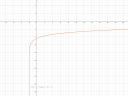
c) `m(x) = log_3(x+2)-5`
Itt megint csak az alap fv-ből érdemes kiindulni, vagyis a `log_3 x`-ből. A logaritmus az exponenciális függvény inverze, vagyis olyan mint az exponenciális fv csak az `y=x` (45°-os jobbra dőlő egyenes) egyenesre tükrözve. Erre inkább csinálok külön ábrát, hogy szemléltessem (4-es ábra). Ami azt jelenti, hogy 0-tól `-oo`-ből jön, 1-nél metszi az `x` tengelyt, aztán szépen lassan folyamatosan nő. Az ábrán látszik, hogy az exponenciális tükörképe. A mi függvényünk viszont ehhez képest el van tolva balra 2-vel és lefele 5-tel. Ami azt jelenti, hogy -2-ből fog lentről jönni a fv. Aztán 1-nél lenne 0 az értéke, de itt `1-2=-1`-nél lesz `0-5=-5` az értéke és utána elmegy jobbra a fv.
2.
a)
`cos(x-pi/3) = 1/2 " /"cos^"-1"()`
`"I."`
`x_1-pi/3 = pi/3+k*2 pi", "k in ZZ " /"+pi/3`
`x_1 = (2 pi)/3+k*2 pi", "k in ZZ`
`"II."`
`x_2-pi/3 = -pi/3+k*2 pi", "k in ZZ " /"+pi/3`
`x_2 = 0+k*2 pi", "k in ZZ`
b)
`sin(x+pi/3) = sqrt(2)/2 " /"sin^"-1"()`
`"I."`
`x_1+pi/3 = pi/4+k*2 pi", "k in ZZ " /"-pi/3`
`x_1 = -pi/12+k*2 pi", "k in ZZ`
`"II."`
`x_2+pi/3 = (3 pi)/4+k*2 pi", "k in ZZ " /"-pi/3`
`x_2 = (5 pi)/12+k*2 pi", "k in ZZ`
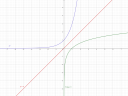
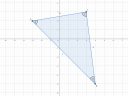
3. `A(-3"; " 2)", " B(4"; " -5)", " C(3"; " 3)`
Nevezzük az `A, B, C` csúcsokkal szembeni oldalakat rendre `a, b, c`-nek és a csúcsoknál lévő szögeket `alpha, beta, gamma`-nek. De az 5-ös ábrán is látszik!
`a = abs(BC) = sqrt((4-3)^2+(3-(-5))^2) = sqrt(1^2+8^2) = sqrt 65`
`b = abs(AC) = sqrt((3-(-3))^2+(3-2)^2) = sqrt(6^2+1^2) = sqrt 37`
`c = abs(AB) = sqrt((4-(-3))^2+(2-(-5))^2) = sqrt(7^2+7^2) = sqrt(2*7^2) = 7 sqrt 2`
(Itt mindegy, hogy melyikből vonjuk ki melyiket, mert a ugyanannyi lesz a négyzete mindkettőnek, ezért én úgy szoktam, hogy mindig pozitívra jöjjön ki a különbség.)
Ezzel megvan az összes oldal hossza, viszont nekünk a szögek kellenek. Ilyenkor, amikor csak az oldalak vannak meg, ilyenkor a koszinusztételt kell alkalmaznunk, mert ahhoz 3 oldal kell és 1 szög, ami pont ideális nekünk. mondjuk `alpha`-ra:
`a^2 = b^2+c^2-2bc cos alpha => cos alpha = (b^2+c^2-a^2)/(2bc)`
Vagyis
`alpha = cos^"-1"((b^2+c^2-a^2)/(2bc)) ``=`` cos^"-1"((37+2*7^2-65)/(2 sqrt(37)*7sqrt(2))) ``=`` cos^"-1"(5/sqrt(74)) ~~ "54,462"°`
Ha pedig van már egy szögünk, akkor használhatjuk a szinusztételt, amihez 2 oldal és 2 szög kell:
`sin beta/sin alpha = b/a => sin beta = (b sin alpha)/a`
Tehát
`beta = sin^"-1"((b sin alpha)/a) ``=`` sin^"-1"((sqrt(37)*7/sqrt(74))/sqrt(65)) ``=`` sin^"-1"((7 cancel sqrt 37)/sqrt(2*cancel 37*65)) ``=`` sin^"-1"(7/(sqrt(130))) ~~ "37,875"°`
Az utolsó fok pedig már adódik, mert a belső szögek összege 180°:
`gamma = 180-alpha-beta ~~ "87,663"`
A területre pedig ott van az általános képlet, amihez két oldal és a köztük lévő szög kell. Például:
`T=(ab sin gamma)/2 = (sqrt 65*sqrt 37*49/sqrt(2405))/2 = 49/2 = "24,5"`
4.
a)
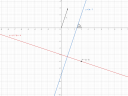
`y = 3x-7`
Ebből az alakból közvetlenül leolvasható az egyenes meredeksége `m = 3`. Az irányvektor és a meredekség kapcsolata pedig a következő. Ha az irányvektor koordinátái `"v"(v_1; v_2)`, akkor a meredekség
`m = v_2/v_1`
Mivel itt a meredekség 3, ezért
`3/1 = v_2/v_1`
Vagyis az irányvektor:
`"v"(v_1; v_2) = (1; 3)`
Az irányszög (`alpha`), az pedig az a szög, amit az egyenes bezár az `x` tengellyel. Szokták -90° és 90° és 0° és 180° között is értelmezni. Én most ez előbbi szerint fogom. Az előbb megvizsgált meredekségnek a másik neve "iránytangens", ugyanis az pont ennek a szögnek a tangense, vagyis
`m = "tg"\ alpha = 3 => alpha = "tg"^"-1"\ 3 ~~ "71,565"°`
b) `P(3; -5)`
Egy adott meredekségre úgy kapunk merőleges meredekséget, hogy a meredekség mínusz reciprokát vesszük. Jelen esetben:
`m_2 = -1/m = -1/3`
Ez lesz az előző egyenesre merőleges meredekség. Innentől pedig már csak az adott ponton áthaladó, adott meredekségű egyenes egyenletét kell felírni, ami
`y-(-5) = -1/3(x-3)`
`y+5 = -1/3 x+1 " /"-5`
`y = -1/3 x-4`
Jó sok mindenről esett szó! Ha bármi kérdésed lenne nyugodtan kérdezz!
a) `f(x) = x^2-5x-8`
Ez egy parabola, vagyis egy másodfokú polinom, ami azt jelenti, hogy ha az `x^2`-es tag pozitív, akkor `uu` alakú a függvény képe, ha negatív, akkor pedig `nn` alakú. Itt pozitív, szóval van neki egy minimuma. Ha egy kicsit átalakítjuk a teljes négyzetes formájába akkor leolvasható róla a minimuma:
`x^2-5x-8 = (x-5/2)^2-25/4-8 = (x-5/2)^2-57/4`
A függvénytranszformációkat ismerve láthatjuk, hogy ez az eredeti `x^2` függvény eltolva jobbra `5/2`-del és lefele `57/4`-del, vagyis a `T(5/2"; " -57/4)` pontban van az U alak csúcsa és onnan ível szépen felfelé. Ami azt is jeleni, hogy `5/2`-ig csökken a függvény értéke és utána pedig nő.
b) `g(x) = 3^(x-2)-5`
Ez egy exponenciális függvény, ami azt jelenti negatív számokra nagyon kicsi a fv értéke, viszont pozitív irányba nagyon hamar megugrik. Vagyis alapból a `3^x` balról a 0-ból jön, az `y` tengelyhez érve 1 az értéke, majd pedig szinte azonnal felfele kanyarodik és megy a `oo`-be. Ez a függvény viszont el van tolva jobbra 2-vel és lefele 5-tel. Vagyis ez -5-ből jön és majd csak `x=2`-nél lesz az értéke `1-5 = -4` (mivel -5-tel el van tolva) és utána ugyanúgy elhúz a végtelenbe. Illetve a fv az egész tartományán növekvő.
c) `m(x) = log_3(x+2)-5`
Itt megint csak az alap fv-ből érdemes kiindulni, vagyis a `log_3 x`-ből. A logaritmus az exponenciális függvény inverze, vagyis olyan mint az exponenciális fv csak az `y=x` (45°-os jobbra dőlő egyenes) egyenesre tükrözve. Erre inkább csinálok külön ábrát, hogy szemléltessem (4-es ábra). Ami azt jelenti, hogy 0-tól `-oo`-ből jön, 1-nél metszi az `x` tengelyt, aztán szépen lassan folyamatosan nő. Az ábrán látszik, hogy az exponenciális tükörképe. A mi függvényünk viszont ehhez képest el van tolva balra 2-vel és lefele 5-tel. Ami azt jelenti, hogy -2-ből fog lentről jönni a fv. Aztán 1-nél lenne 0 az értéke, de itt `1-2=-1`-nél lesz `0-5=-5` az értéke és utána elmegy jobbra a fv.
2.
a)
`cos(x-pi/3) = 1/2 " /"cos^"-1"()`
`"I."`
`x_1-pi/3 = pi/3+k*2 pi", "k in ZZ " /"+pi/3`
`x_1 = (2 pi)/3+k*2 pi", "k in ZZ`
`"II."`
`x_2-pi/3 = -pi/3+k*2 pi", "k in ZZ " /"+pi/3`
`x_2 = 0+k*2 pi", "k in ZZ`
b)
`sin(x+pi/3) = sqrt(2)/2 " /"sin^"-1"()`
`"I."`
`x_1+pi/3 = pi/4+k*2 pi", "k in ZZ " /"-pi/3`
`x_1 = -pi/12+k*2 pi", "k in ZZ`
`"II."`
`x_2+pi/3 = (3 pi)/4+k*2 pi", "k in ZZ " /"-pi/3`
`x_2 = (5 pi)/12+k*2 pi", "k in ZZ`
3. `A(-3"; " 2)", " B(4"; " -5)", " C(3"; " 3)`
Nevezzük az `A, B, C` csúcsokkal szembeni oldalakat rendre `a, b, c`-nek és a csúcsoknál lévő szögeket `alpha, beta, gamma`-nek. De az 5-ös ábrán is látszik!
`a = abs(BC) = sqrt((4-3)^2+(3-(-5))^2) = sqrt(1^2+8^2) = sqrt 65`
`b = abs(AC) = sqrt((3-(-3))^2+(3-2)^2) = sqrt(6^2+1^2) = sqrt 37`
`c = abs(AB) = sqrt((4-(-3))^2+(2-(-5))^2) = sqrt(7^2+7^2) = sqrt(2*7^2) = 7 sqrt 2`
(Itt mindegy, hogy melyikből vonjuk ki melyiket, mert a ugyanannyi lesz a négyzete mindkettőnek, ezért én úgy szoktam, hogy mindig pozitívra jöjjön ki a különbség.)
Ezzel megvan az összes oldal hossza, viszont nekünk a szögek kellenek. Ilyenkor, amikor csak az oldalak vannak meg, ilyenkor a koszinusztételt kell alkalmaznunk, mert ahhoz 3 oldal kell és 1 szög, ami pont ideális nekünk. mondjuk `alpha`-ra:
`a^2 = b^2+c^2-2bc cos alpha => cos alpha = (b^2+c^2-a^2)/(2bc)`
Vagyis
`alpha = cos^"-1"((b^2+c^2-a^2)/(2bc)) ``=`` cos^"-1"((37+2*7^2-65)/(2 sqrt(37)*7sqrt(2))) ``=`` cos^"-1"(5/sqrt(74)) ~~ "54,462"°`
Ha pedig van már egy szögünk, akkor használhatjuk a szinusztételt, amihez 2 oldal és 2 szög kell:
`sin beta/sin alpha = b/a => sin beta = (b sin alpha)/a`
Tehát
`beta = sin^"-1"((b sin alpha)/a) ``=`` sin^"-1"((sqrt(37)*7/sqrt(74))/sqrt(65)) ``=`` sin^"-1"((7 cancel sqrt 37)/sqrt(2*cancel 37*65)) ``=`` sin^"-1"(7/(sqrt(130))) ~~ "37,875"°`
Az utolsó fok pedig már adódik, mert a belső szögek összege 180°:
`gamma = 180-alpha-beta ~~ "87,663"`
A területre pedig ott van az általános képlet, amihez két oldal és a köztük lévő szög kell. Például:
`T=(ab sin gamma)/2 = (sqrt 65*sqrt 37*49/sqrt(2405))/2 = 49/2 = "24,5"`
4.
a)
`y = 3x-7`
Ebből az alakból közvetlenül leolvasható az egyenes meredeksége `m = 3`. Az irányvektor és a meredekség kapcsolata pedig a következő. Ha az irányvektor koordinátái `"v"(v_1; v_2)`, akkor a meredekség
`m = v_2/v_1`
Mivel itt a meredekség 3, ezért
`3/1 = v_2/v_1`
Vagyis az irányvektor:
`"v"(v_1; v_2) = (1; 3)`
Az irányszög (`alpha`), az pedig az a szög, amit az egyenes bezár az `x` tengellyel. Szokták -90° és 90° és 0° és 180° között is értelmezni. Én most ez előbbi szerint fogom. Az előbb megvizsgált meredekségnek a másik neve "iránytangens", ugyanis az pont ennek a szögnek a tangense, vagyis
`m = "tg"\ alpha = 3 => alpha = "tg"^"-1"\ 3 ~~ "71,565"°`
b) `P(3; -5)`
Egy adott meredekségre úgy kapunk merőleges meredekséget, hogy a meredekség mínusz reciprokát vesszük. Jelen esetben:
`m_2 = -1/m = -1/3`
Ez lesz az előző egyenesre merőleges meredekség. Innentől pedig már csak az adott ponton áthaladó, adott meredekségű egyenes egyenletét kell felírni, ami
`y-(-5) = -1/3(x-3)`
`y+5 = -1/3 x+1 " /"-5`
`y = -1/3 x-4`
Jó sok mindenről esett szó! Ha bármi kérdésed lenne nyugodtan kérdezz!

1
-
bartam34: Köszönök mindent!
 3 éve
1
3 éve
1
-
bartam34: Az első feladatra még ráférne egy tisztázás! De a többi jó! 3 éve 0
 Epyxoid
{ Tanár }
válasza
Epyxoid
{ Tanár }
válasza
Milyen tisztázásra gondolsz az 1-es feladatban? Tudok valahogy segíteni? 

0
- Még nem érkezett komment!