Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Elipszis érintő egyenlete
 Törölt
{ Kérdező } kérdése
Törölt
{ Kérdező } kérdése
353
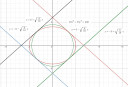
Határozzuk meg a 16x² + 25y² = 400 elipszis és az x² + y² = 20 kör közös értintőinek az egyenletét.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2 kazah
válasza
kazah
válasza
Mivel mindkét alakzat origó középpontú, négy egyenes egyenletet fogunk találni.
Írjuk fel a kör érintőinek általános egyenletét:
`(mx+b)^2+x^2=20`
`x^2*(m^2+1)+x*2mb+b^2-20=0`
diszkrimináns nulla:
`(2mb)^2-4*(m^2+1)*(b^2-20)=0`
`m^2-(m^2b^2+b^2-20m^2-20)=0`
`m^2(1-b^2+20)+20-b^2=0`
`m^2=(b^2-20)/(1-b^2+20)`
Ugyanezt az ellipszisre:
`16x^2+25(mx+b)^2=400`
`16x^2+25m^2x^2+50mbx+25b^2-400=0`
itt is nulla a diszkrimináns:
`(50mb)^2-4*(16+25m^2)(25b^2-400)=0`
`cancel(2500m^2b^2)-cancel(2500m^2b^2)-1600b^2+25600+40000m^2=0`
`16b^2-256=400m^2`
`m^2=(16b^2-256)/400`
`b^2=a` helyettesítéssel:
`(16a-256)/400=a/20-1`
a-ra megoldod, a=36
`b=pm6` `rightarrow` m= visszahelyettesítesz. `root()((6^2-256)/400)` = `root()(8/10)` (plusz és minusz)
A négy egyenlet egybegyúrva:
`y = pm 6 pm root()(8/10)*x`
Írjuk fel a kör érintőinek általános egyenletét:
`(mx+b)^2+x^2=20`
`x^2*(m^2+1)+x*2mb+b^2-20=0`
diszkrimináns nulla:
`(2mb)^2-4*(m^2+1)*(b^2-20)=0`
`m^2-(m^2b^2+b^2-20m^2-20)=0`
`m^2(1-b^2+20)+20-b^2=0`
`m^2=(b^2-20)/(1-b^2+20)`
Ugyanezt az ellipszisre:
`16x^2+25(mx+b)^2=400`
`16x^2+25m^2x^2+50mbx+25b^2-400=0`
itt is nulla a diszkrimináns:
`(50mb)^2-4*(16+25m^2)(25b^2-400)=0`
`cancel(2500m^2b^2)-cancel(2500m^2b^2)-1600b^2+25600+40000m^2=0`
`16b^2-256=400m^2`
`m^2=(16b^2-256)/400`
`b^2=a` helyettesítéssel:
`(16a-256)/400=a/20-1`
a-ra megoldod, a=36
`b=pm6` `rightarrow` m= visszahelyettesítesz. `root()((6^2-256)/400)` = `root()(8/10)` (plusz és minusz)
A négy egyenlet egybegyúrva:
`y = pm 6 pm root()(8/10)*x`
1
-
Epyxoid: Az `(16a-256)/400=a/20-1` egyenlet szerintem első ránézésre nem érthető honnan származik, de egyébként szép kis villám levezetés!
 3 éve
0
3 éve
0
-
kazah: ja, már azt se tudom, hogy mit hagytam ki belőle, de a megoldás menete nagyjából követhető (én tudtam követni
 )
3 éve
0
)
3 éve
0
 Epyxoid
{ Tanár }
válasza
Epyxoid
{ Tanár }
válasza
A számolást kicsit részletezve:
`(2mb)^2-4(m^2+1)(b^2-20) = 0`
`4m^2 b^2-4(m^2 b^2-20m^2+b^2-20) = 0`
`cancel(4m^2 b^2) cancel(-4m^2 b^2)+80m^2-4b^2+80 = 0 " /"+4b^2`
`4b^2 = 80(m^2+1) " /":4`
`b^2 = 20(m^2+1)`
`(50mb)^2-4(25m^2+16)(25b^2-400) = 0`
`(50mb)^2-4*25(25m^2+16)(b^2-16) = 0 " /":100`
`cancel(25m^2 b^2) cancel(-25m^2 b^2)+400m^2-16b^2+256 = 0 " /"+16b^2`
`16b^2 = 16(25m^2+16) " /":16`
`b^2 = 25m^2+16`
`20m^2+20 = 25m^2+16 " /"-20m^2-16`
`5m^2 = 4 " /":5`
`m^2 = 4/5 " /"sqrt`
`m = +-sqrt(4/5)`
`b^2 = 20(4/5+1)`
`b^2 = cancel 20_4*9/cancel 5`
`b^2 = 36 " /"sqrt`
`b = +-6`
`(2mb)^2-4(m^2+1)(b^2-20) = 0`
`4m^2 b^2-4(m^2 b^2-20m^2+b^2-20) = 0`
`cancel(4m^2 b^2) cancel(-4m^2 b^2)+80m^2-4b^2+80 = 0 " /"+4b^2`
`4b^2 = 80(m^2+1) " /":4`
`b^2 = 20(m^2+1)`
`(50mb)^2-4(25m^2+16)(25b^2-400) = 0`
`(50mb)^2-4*25(25m^2+16)(b^2-16) = 0 " /":100`
`cancel(25m^2 b^2) cancel(-25m^2 b^2)+400m^2-16b^2+256 = 0 " /"+16b^2`
`16b^2 = 16(25m^2+16) " /":16`
`b^2 = 25m^2+16`
`20m^2+20 = 25m^2+16 " /"-20m^2-16`
`5m^2 = 4 " /":5`
`m^2 = 4/5 " /"sqrt`
`m = +-sqrt(4/5)`
`b^2 = 20(4/5+1)`
`b^2 = cancel 20_4*9/cancel 5`
`b^2 = 36 " /"sqrt`
`b = +-6`
0
- Még nem érkezett komment!