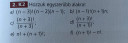Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Kombinatorika - permutációk
 Kitti13
kérdése
Kitti13
kérdése
416
Sziasztok!
Segítséget szeretnék kérni az alábbi feladatokban. Már 2-3 órája próbálkozom, de nem jutok egyről a kettőre.
Előre is köszönöm a segítséget.
Segítséget szeretnék kérni az alábbi feladatokban. Már 2-3 órája próbálkozom, de nem jutok egyről a kettőre.
Előre is köszönöm a segítséget.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2 kazah
válasza
kazah
válasza
Három egymást követő természetes szám szorzata 60, melyik lehet.
`3*4*5`
Eredetileg 5 volt, akkor a permutációk száma 5! = 120
Lett 2, akkor pedig 2! = 2
a,
`(n-3)!*(n-2)*(n-1)` = `(n-1)!`
b,
`(n-1)!*n*(n+1)` = `(n+1)!`
c,
`((n+3)!)/(n+3)` = `(n+2)!`
d,
`((n+3)!)/((n+1)!)` = `(n+2)*(n+3)`
e,
`n!+(n+1)!` = `n!*(1+n+1)` = `n!*(n+2)`
f,
`(n+1)!-n!` = `n!*((n+1)-1)` = `n*n!`
Módosítva: 3 éve
1
-
Epyxoid: A d az `((n+3)!)/((n+1)!)`, tehát csak `(n+3)(n+2)` lesz. 3 éve 0
-
kazah: igen, javítom, köszi
 3 éve
0
3 éve
0
-
Epyxoid: Egyébként az e-nél és az f-nél hogy hozol szorzat alakra? 3 éve 0
-
kazah: `(n+1)!` = `n!*(n+1)` 3 éve 1
-
Epyxoid: Jaaaaaa, átírta és kiemeltél! Te jó ég, szerintem egy év alatt se esett volna le

 Köszi! Tök jó!
3 éve
0
Köszi! Tök jó!
3 éve
0
-
kazah: Dehogynem, rájöttél volna nélkülem is
 3 éve
0
3 éve
0
-
Epyxoid: Hát nem tudom
 Nagyon néztem, de nem akart összejönni
Nagyon néztem, de nem akart összejönni  3 éve
0
3 éve
0
 Epyxoid
{ Tanár }
válasza
Epyxoid
{ Tanár }
válasza
A 12. K2-höz még annyit hozzátennék, hogy ha elnevezzük az elemszámot `n`-nek, akkor
`(n!)/((n-3)!) = 60`
`n(n-1)(n-2) = 60`
Azaz három egymásutáni számot kell keresnünk, aminek a szorzata 60. Próbálgatással rá lehet találni a 3,4,5-re, vagyis
`(5!)/((5-3)!) = (5*4*3*cancel(2*1))/cancel(2*1) = 5*4*3 = 60`
Tehát 5 eleme volt eredetileg a halmaznak.
(Tudom, hogy ugyanezt írtad kazah, de nagyon hamar belecsaptál a közepébe. Gondoltam így érthetőbb. )
)
`(n!)/((n-3)!) = 60`
`n(n-1)(n-2) = 60`
Azaz három egymásutáni számot kell keresnünk, aminek a szorzata 60. Próbálgatással rá lehet találni a 3,4,5-re, vagyis
`(5!)/((5-3)!) = (5*4*3*cancel(2*1))/cancel(2*1) = 5*4*3 = 60`
Tehát 5 eleme volt eredetileg a halmaznak.
(Tudom, hogy ugyanezt írtad kazah, de nagyon hamar belecsaptál a közepébe. Gondoltam így érthetőbb.
 )
)
Módosítva: 3 éve
1
-
kazah: Igen, mert full paraméteresen nagyon harmadfokú, nem akartam belemerülni
 3 éve
0
3 éve
0
-
Epyxoid: Igen, attól én is megijedtem
 De azért nem árt a plusz magyarázat.
De azért nem árt a plusz magyarázat.  3 éve
0
3 éve
0
-
kazah: Az sosem árt
 3 éve
1
3 éve
1