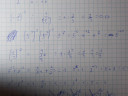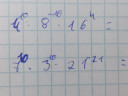Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Hatványozás ellenőrzés
 kakimarci6
kérdése
kakimarci6
kérdése
355
Sziasztok. A matekházimat szeretném ha leellenőriznétek és ha van valami hiba akkor azt elmagyarázni. Ja és van még kettő olyan feladat amit nem tudtam megoldani.. ebben is kérek egy kis segítséget.
Jelenleg 1 felhasználó nézi ezt a kérdést.
1
Középiskola / Matematika
Válaszok
1 Epyxoid
{ Tanár }
válasza
Epyxoid
{ Tanár }
válasza
Majdnem jó, de nem teljesen az.
Törttel úgy osztunk, hogy a reciprokával szorzunk.
`(-2/3)^(-1) = 1/(-2/3)^1 = 1 : (-2/3) = 1*(-3/2) = -3/2`
Hatványnak a hatványát összeszorozzuk és mínusz x mínusz az plusz.
`(5^(-3))^(-2)*(5^4)^(-3)*5^7 = 5^((-3)*(-2))*5^(4*(-3))*5^7 = 5^6*5^(-12)*5^7 = 5^(6-12+7) = 5`
Itt ugyanaz a hiba, mint az elsőnél.
`(1/3)^(-2) = 1/((1/3)^2) = 1:1^2/3^2 = 1*9/1 = 9`
Na itt pedig már egy kicsit belekeveredtél. Mutatom, hogy ez hogyan nézne ki:
`5^(-1)+2^(-3) = 1/5^1+1/2^3 = ( 1:5^1+1:2^3 = 1*1/5^1+1*1/2^3 =)\ 1/5+1/8 = 8/40+5/40 = 13/40`
Vagyis egész számoknál nem ér semmit a reciprokkal való szorzás, mert ugyanazt kapjuk vissza. Semmi sem egyszerűsödik.
Itt is ugyanaz csak a hiba.
`5^0-5^(-1) = 1-1/5^1 = 1-1/5 = 5/5-1/5 = 4/5`
Amiben megakadtál ott pedig csak annyit kell csinálni, hogy felbontod az összetett számokat prímekké és egyszerűbb alakra hozod a kifejezést!
`4^10*8^(-16)*16^4 = (2^2)^10*(2^3)^(-16)*(2^4)^4 = 2^(20-48+16) = 2^(-12)`
Itt viszont két dolgot is csinálhatunk. Mivel `3*7=21`, és mivel a 3 és a 7 is azonos hatványon van, ezért összevonhatjuk `21^10`-é az első két tagot, vagy pedig a `21^(-21)`-t bontjuk szét `3^(-21)*7^(-21)`-re. Szerintem inkább az utóbbi a célszerű, de a másik is jó lehet.
`7^10*3^10*21^(-21) = 7^10*3^10*(3*7)^(-21) = 7^10*3^10*3^(-21)*7^(-21) = 3^(10-21)*7^(10-21) = 3^(-11)*7^(-11)\ (= 21^(-11))`
Ennyi az egész! Szólj nyugodtan, ha bármi kérdésed lenne!
Törttel úgy osztunk, hogy a reciprokával szorzunk.
`(-2/3)^(-1) = 1/(-2/3)^1 = 1 : (-2/3) = 1*(-3/2) = -3/2`
Hatványnak a hatványát összeszorozzuk és mínusz x mínusz az plusz.
`(5^(-3))^(-2)*(5^4)^(-3)*5^7 = 5^((-3)*(-2))*5^(4*(-3))*5^7 = 5^6*5^(-12)*5^7 = 5^(6-12+7) = 5`
Itt ugyanaz a hiba, mint az elsőnél.
`(1/3)^(-2) = 1/((1/3)^2) = 1:1^2/3^2 = 1*9/1 = 9`
Na itt pedig már egy kicsit belekeveredtél. Mutatom, hogy ez hogyan nézne ki:
`5^(-1)+2^(-3) = 1/5^1+1/2^3 = ( 1:5^1+1:2^3 = 1*1/5^1+1*1/2^3 =)\ 1/5+1/8 = 8/40+5/40 = 13/40`
Vagyis egész számoknál nem ér semmit a reciprokkal való szorzás, mert ugyanazt kapjuk vissza. Semmi sem egyszerűsödik.
Itt is ugyanaz csak a hiba.
`5^0-5^(-1) = 1-1/5^1 = 1-1/5 = 5/5-1/5 = 4/5`
Amiben megakadtál ott pedig csak annyit kell csinálni, hogy felbontod az összetett számokat prímekké és egyszerűbb alakra hozod a kifejezést!
`4^10*8^(-16)*16^4 = (2^2)^10*(2^3)^(-16)*(2^4)^4 = 2^(20-48+16) = 2^(-12)`
Itt viszont két dolgot is csinálhatunk. Mivel `3*7=21`, és mivel a 3 és a 7 is azonos hatványon van, ezért összevonhatjuk `21^10`-é az első két tagot, vagy pedig a `21^(-21)`-t bontjuk szét `3^(-21)*7^(-21)`-re. Szerintem inkább az utóbbi a célszerű, de a másik is jó lehet.
`7^10*3^10*21^(-21) = 7^10*3^10*(3*7)^(-21) = 7^10*3^10*3^(-21)*7^(-21) = 3^(10-21)*7^(10-21) = 3^(-11)*7^(-11)\ (= 21^(-11))`
Ennyi az egész! Szólj nyugodtan, ha bármi kérdésed lenne!

Módosítva: 3 éve
0
-
kakimarci6: Köszönöm hogy időt szántál rám 3 éve 1
-
Epyxoid: Nagyon szívesen! 3 éve 0
-
Epyxoid: Amúgy is te vagy az első itt, aki legalább megpróbálta megoldani a saját feladatait, szóval hatalmas tisztelet! Mások csak felteszik ide úgy, hogy neki se kezdenek maguktól... 3 éve 0