Mégse tudok segíteni ebben.

a,

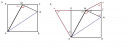
A rajz sokat segít.

Az AMD szög az A csúcsnál levő szög pótszöge, 90-u.

Az M pontnál levő egyenes szög:

`u+x+(90-u)=180`

x = 90°, az AMN szög derékszög.

b,

`bar(CD)=2*root()(3)` cm `rightarrow` `bar(DM)=bar(MC)=root()(3)` cm

Egészítsük ki a derékszögű háromszögeket, tükrözve az oldalakra (ábra).

Mindkét esetben egyenlő oldalú háromszögeket kapunk.

`bar(MM')` = `bar(MA)` = `2*root()(3)`

`bar(AD)` = `root()((AM)^2-(DM)^2)` = `root()((2*root()(3))^2-root()(3)^2)` = `root()(12-3)` = `root()(9)` = 3 cm

A téglalap területét mostmár ki tudjuk számolni:

`T_t` = `bar(AD)*bar(CD)` = `3*2*root()(3)` = `6*root()(3)` `cm^2`

Az MNN' egyenlő oldalú háromszögnek a magasságát ismerjük, tovább azt, hogy

`bar(NC)` = `bar(N'C)` = `bar(MN)/2`

`bar(MC)` = `root()((MN)^2-(NC)^2)` = `root()((MN)^2-((MN)/2)^2)` = `root()(3/4*(MN)^2)` = `root()(3)/2*bar(MN)`

`root()(3)` = `root()(3)/2*bar(MN)`

`bar(MN)=(2*root()(3))/root()(3)` = 2 cm

Az AMN háromszög területe:

`T_h` = `((AM)*(MN))/2` = `(2*root()(3)*2)/2` = `2*root()(3)` `cm^2`

A két terület aránya:

`T_h/T_t` = `(2*root()(3))/(6*root()(3))` = `2/6` = `1/3`

Próbáltam szinusz nélkül, ha már általános iskolás a feladat.