Holnap segítek!

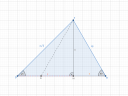
A magyarázatomhoz nagy szükség van az ábrára, amit mellékelek. Azt mindenképp nézd mellé!

Az `FM` magasság két nevezetes háromszögre osztja szét a `DEF` háromszöget: a `DMF` egy 45-45-90 fokos egyenlő szárú derékszögű háromszög, vagyis egy "fél négyzet", tehát `abs(DM)=abs(FM)`; illetve az `EMF` egy 30-60-90 fokos derékszögű háromszög, ami pont egy egyenlő oldalú háromszög fele, vagyis `abs(EM)=abs(EF)/2`. Első körben ennyit érdemes észrevenni.

a)
Aztán azt érdemes tudni, hogy egy négyzet átlója az a `sqrt2`-szöröse a négyzet oldalának, vagyis jelen esetben, mivel `DF` egy fél négyzet átlója, aminek az oldalai a `DM` és az `FM`, ezért ezeknek a hossza 3 lesz, hiszen ennek a `sqrt2`-szöröse a `3 sqrt 2`. De ezt máshogy, mindenféle rálátás nélkül is beláthatjuk: mivel a `DMF` háromszögben 2 szög is ismert, ezért tudjuk a harmadikat is, ami ugyanúgy 45° lesz (180-90-45), mint a `D` csúcsnál, és mivel azonos szögekhez, azonos szemközti oldalak társulnak, így tudjuk, hogy `abs(DM)=abs(FM)`. Ha ezt a hosszt elnevezzük mondjuk `x`-nek, akkor felírva a Pitagoraszt a `DMF` háromszögre a következőt kapjuk:
`abs(DF)^2 = abs(DM)^2+abs(FM)^2 = x^2+x^2 = 2x^2`

Ebből ha kifejezzük az `x`-et, akkor `x=abs(DF)/sqrt 2`-t kapunk és mivel `abs(DF) = 3 sqrt 2`, így
`x = (3 sqrt 2)/sqrt 2 = 3`
De ha csak behelyettesítesz a `abs(DF)^2 = 2x^2` képletbe, abból is megkapod, hogy x = 3, vagyis az `FM` magasság hossza az 3.

b)
Mivel általános iskolainak soroltad be a feladatot, ezért itt az egyenlő oldalú háromszög meglátása nélkül nem igazán tudom hogyan máshogy tudnám még megmagyarázni a feladat menetét (trigonometria nélkül), úgyhogy én ezzel fogok tovább haladni. Az ábrámon bejelöltem azt a `G` pontot, amivel az `FME` háromszög egy egyenlő oldalú háromszöggé egészül ki. Tehát a `abs(GE)=abs(GF)=abs(EF)`, illetve az `abs(EM)` az pont ennek a fele. Ha megint elnevezzük ezt a hosszt, az `abs(EM)` hosszt, ezúttal mondjuk `y`-nak és felírjuk az `FME` háromszögre a Pitagoraszt, akkor ezt kapjuk:
`abs(EF)^2 = abs(FM)^2+abs(EM)^2`
`(2y)^2 = x^2+y^2`
`4y^2 = x^2+y^2 " /"-y^2`
`3y^2 = x^2 " /":3`
`y^2 = x^2/3 " /"sqrt`
`y = x/sqrt 3`

Vagyis az `abs(EM)` hossz az előbb kiszámolt magasság `sqrt3`-ada lesz, az `EF` oldal pedig ennek a kétszerese:
`abs(EM) = y = 3/sqrt 3 = (3 sqrt 3)/3 = sqrt 3`
`abs(EF) = 2y = 2 sqrt 3`

Tehát az `FME` kerülete:
`K_(FME) = abs(FM)+abs(EM)+abs(EF) = m+y+2y = 3+sqrt 3+2 sqrt 3 = 3+3 sqrt 3 ~~ "8,196 cm"`

c)
A `DE` oldalt akaratlanul is kiszámoltuk az a) és b) pont megoldásával:
`abs(DE) = abs(DM)+abs(EM) = x+y = 3+sqrt 3 ~~ "4,732 cm"`, ami nagyobb, mint 4,7 cm!