Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matematika - köszönöm szépen a segítséget!
 edgarallanp.15
kérdése
edgarallanp.15
kérdése
1683
Egy 12,8 cm sugarú gömb egyik síkmetszetének az átmérője:
a, 10,2 cm;
b, 12,8 cm;
c, 21,7 cm;
d, 25,6 cm.
Mekkora távolságra van a metszősík a gömb középpontjától?
Nem hivatalos adatok szerint a 2012-es év legnehezebb dinnyéje az ormánsági Vajszlón termett, és 53 kg-ot nyomott. Körülbelül hány kg lehet a dinnye ehető része, ha a héját 2 cm vastagnak, sűrűségét a víz sűrűségével egyezőnek, az alakját pedig gömbnek vesszük?
Egy gömb alakú dinnyét „párhuzamos síkú vágásokkal” 5 azonos magasságú részre vágtunk szét, az egyes részek (2 gömbszelet és 3 gömbréteg) magassága 4 cm. Mekkora sugarú körök határolják az egyes részeket?
a, 10,2 cm;
b, 12,8 cm;
c, 21,7 cm;
d, 25,6 cm.
Mekkora távolságra van a metszősík a gömb középpontjától?
Nem hivatalos adatok szerint a 2012-es év legnehezebb dinnyéje az ormánsági Vajszlón termett, és 53 kg-ot nyomott. Körülbelül hány kg lehet a dinnye ehető része, ha a héját 2 cm vastagnak, sűrűségét a víz sűrűségével egyezőnek, az alakját pedig gömbnek vesszük?
Egy gömb alakú dinnyét „párhuzamos síkú vágásokkal” 5 azonos magasságú részre vágtunk szét, az egyes részek (2 gömbszelet és 3 gömbréteg) magassága 4 cm. Mekkora sugarú körök határolják az egyes részeket?
Jelenleg 1 felhasználó nézi ezt a kérdést.
Matematika, dinnyematek, Térgeometria
Matematika, dinnyematek, Térgeometria
1
Középiskola / Matematika
Válaszok
1 kazah
megoldása
kazah
megoldása
1,
Egy általános megoldás, majd csak be kell helyettesíteni mindegyik feladatnál.
Ábra
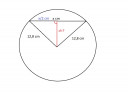
Ott a derékszögű háromszög, az egyik befogója `x/2` cm (az x értékek vannak megadva a részfeladatokban), a másik befogó a kérdés; az átfogó pedig a gömb sugara.
`(x/2)^2+d^2=12.8^2`
d = `root()(12.8^2-(x/2)^2)`
a,
`d_a=root()(12.8^2-(10.2/2)^2)` = 11,74 cm
b,
`d_b=root()(12.8^2-(12.8/2)^2)` = 11,09 cm
c,
`d_c=root()(12.8^2-(21.7/2)^2)` = 6,79 cm
d, Ez azért látszik, hogy nulla, de ki is számolhatjuk.
`d_d=root()(12.8^2-(25.6/2)^2)` = 0 cm (A közepén vágjuk el)
2,
A dinnye térfogata tehát 53 `dm^3`
`V= (4*r^3*pi)/3` `rightarrow` `r=root(3)((3*V)/(4*pi))` = `root(3)((3*53)/(4*3.14))` = 2,33 dm = 23,3 cm
2 cm-rel kisebb a sugara az ehető résznek, vagyis `r_b` = 21,3 cm = 2.13 dm
`V_("ehető")` = `(4*r_b^3*pi)/3` = `(4*2.13^3*3.14)/3` = 40,5 `dm^3`
Vagyis az ehető rész tömege kg 40,5 kg.
3,
Ábra
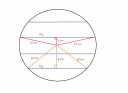
Mint az elsőnél, derékszögű háromszögek.
A gömb átmérője `4*5=20` cm, sugara tehát 10 cm.
`x_1=root()(10^2-2^2)` `approx` 9,8 cm
`x_2=root()(10^2-6^2)` = 8 cm
8 és 9,8 cm sugarú körök lesznek.
Egy általános megoldás, majd csak be kell helyettesíteni mindegyik feladatnál.
Ábra
Ott a derékszögű háromszög, az egyik befogója `x/2` cm (az x értékek vannak megadva a részfeladatokban), a másik befogó a kérdés; az átfogó pedig a gömb sugara.
`(x/2)^2+d^2=12.8^2`
d = `root()(12.8^2-(x/2)^2)`
a,
`d_a=root()(12.8^2-(10.2/2)^2)` = 11,74 cm
b,
`d_b=root()(12.8^2-(12.8/2)^2)` = 11,09 cm
c,
`d_c=root()(12.8^2-(21.7/2)^2)` = 6,79 cm
d, Ez azért látszik, hogy nulla, de ki is számolhatjuk.
`d_d=root()(12.8^2-(25.6/2)^2)` = 0 cm (A közepén vágjuk el)
2,
A dinnye térfogata tehát 53 `dm^3`
`V= (4*r^3*pi)/3` `rightarrow` `r=root(3)((3*V)/(4*pi))` = `root(3)((3*53)/(4*3.14))` = 2,33 dm = 23,3 cm
2 cm-rel kisebb a sugara az ehető résznek, vagyis `r_b` = 21,3 cm = 2.13 dm
`V_("ehető")` = `(4*r_b^3*pi)/3` = `(4*2.13^3*3.14)/3` = 40,5 `dm^3`
Vagyis az ehető rész tömege kg 40,5 kg.
3,
Ábra
Mint az elsőnél, derékszögű háromszögek.
A gömb átmérője `4*5=20` cm, sugara tehát 10 cm.
`x_1=root()(10^2-2^2)` `approx` 9,8 cm
`x_2=root()(10^2-6^2)` = 8 cm
8 és 9,8 cm sugarú körök lesznek.
Módosítva: 3 éve
4
- Még nem érkezett komment!