Question

M értéke, háromszög területe

Károly Hanna kérdése

155 1 éve

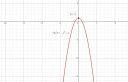
1.Adott az f(x)= -x²-mx+1 függvény. Határozd meg az m valós számot úgy, hogy az f függvény legnagyobb értéke 1 legyen
2.Az XOY koordinátarendszerben adottak: A(-1,3) B(-1,-1) és C(3,3). Határozd meg a háromszög területét

Jelenleg 1 felhasználó nézi ezt a kérdést.

0

Középiskola / Matematika

Válaszok

1

**kazah** megoldása · Accepted Answer · 2022-09-04 15:39:06

1,

`-x^2-mx+1` = `-(x^2+mx)+1` = `-(x+m/2)^2+m^2/4+1`

A `-(x+m/2)^2` maximális értéke nulla.

Akkor `m^2/4+1=1` /-1

`m^2/4=0`

`m^2=0`

m=0

Ekkor a függvény: `f(x)=-x^2+1` lesz, maximális értéke pedig 1.

2,

`m_(AB)` = `(y_B-y_A)/(x_B-x_A)` = `(-1-3)/(-1-(-1))` = `-4/0` = `oo`

`m_(AC)` = `(y_C-y_A)/(x_C-x_A)` = `(3-3)/(3-(-1))` = `0/4` = 0

A két oldal merőleges; a háromszög derékszögű.

`d_(AB)` = `root()((x_B-x_A)^2+(y_B-y_A)^2)` = `root()((-1-(-1))^2+(-1-3)^2)` = `root()(4^2)` = 4

`d_(AC)` = `root()((x_C-x_A)^2+(y_C-y_A)^2)` = `root()(3-(-1))^2+(3-3)^2)` = `root()(4^2)` = 4

`T_(ABC)` = `(d_(AB)*d_(AC))/2` = `(4*4)/2` = 8

Keresés

Toplista

M értéke, háromszög területe

Válaszok