Keresés


Toplista

Toplista
  • betöltés...

Magántanár kereső

Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!

Olaj tartály

160
Egy 84 cm belső átmérőjű, fekvő körhenger alakú olajtartályból elfogyott az olaj egy része. A tartály oldalán lévő mérce azt jelzi, hogy a tartályban 65 cm magasan áll az olaj. A tartály belső hossza 315 cm. Hány liter olaj van a tartályban? (1449 liter a megoldás csak nem tudom hogyan jön ki)
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika

Válaszok

1

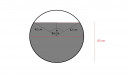
A rajz sokat segít.

Ott a fekvő hordó keresztmetszete.

d = 84 cm `rightarrow` r = 42 cm

Számoljuk ki a levegő térfogatát, aztán kivonjuk a teljes térfogatból.

A keresztmetszeten egy körszelet területe lesz a levegő. Az egyenlőszárú háromszög magassága 65-42 = 23 cm

`cos(alpha/2)=m/r` = `23/42` = 0,548

`alpha/2` = 56,8°

`alpha=2*56.8` = 113,6°.

A háromszög területe:

`T_h` = `(r^2*sinalpha)/2` = `(42^2*sin113.6)/2` = 808,28 `cm^2`

A körcikk területe:

`T_(kc)` = `(r^2*pi*alpha)/360` = `(42^2*3.14*113.6)/360` = 1748,7 `cm^2`

A körszelet területe:

`T_(ksz)` = `T_(kc)-T_h` = `1748.7-808.28` = 940,5 `cm^2`

Az olaj felülete tehát:

`T_("olaj")` = `T_k-T_(ksz)` = `r^2*pi-T_(ksz)` = `42^2*3.14-940.5` = 4601 `cm^2`

h = 315 cm

`V_("olaj")` = `T_("olaj")*h` = `4601*315` = 1 449 414 `cm^3` = 1449 `dm^3` olaj van benne.
Válasz kép
1