Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matek házi
 jozsefattila
kérdése
jozsefattila
kérdése
360
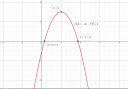
f(x)= -(x-2)ˇ2+3
Zérushely: ?
Szélsőérték: ?
Monotonitás: ?
Zérushely: ?
Szélsőérték: ?
Monotonitás: ?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 kazah
megoldása
kazah
megoldása
`f(x)=-(x-2)^2+3`
Függvénytranszformációk:
- `f(x)=x^2` alapfüggvény (parabola)
- `f(x)=(x-2)^2` eltolás az x tengely mentén pozitív irányba 2 egységgel (jobbra)
- `f(x)=-(x-2)^2` tükrözés az x tengelyre
- `f(x)=-(x-2)^2+3` eltolás az y tengely mentén pozitív irányba 3 egységgel (felfelé)
Az alapfüggvényt tehát a (érdemes a csúcspontot, ami alapfüggvény esetén a (0;0) ) eltoltuk a (2;3) pontba és tükröztük (lefelé nyíló parabola lett belőle).
Értelmezési tartomány: `x in RR`
Értékkészlet: `f(x) in RR`, `f(x) in [-oo;3[`
Zérushely: Ahol a függvény értéke nulla.
`-(x-2)^2+3=0` /`color(red)("-3")`
`-(x-2)^2=-3` /`color(red)(*(-1))`
`(x-2)^2=3` /`color(red)("gyökvonás")`
I. `x-2=root()(3)` `rightarrow` `x_1` = `root()(3)+2` `approx` 3,732
II. `x-2=-root()(3)` `rightarrow` `x_2` = `2-root()(3)` `approx` 0,268
A két zérushely a `2+root()(3)` és a `2-root()(3)`.
Szélsőérték: Már megállapítottuk a függvénytranszformációk során; ha lefelé nyíló a parabola, akkor maximuma van, mégpedig a (2;3) pontban.
Monotonitás:
A lefelé nyíló parabolák a szélsőértékig növekednek, utána csökkennek.
Szigorúan monoton növekvő: `x in ]-oo;2]`
Szigorúan monoton csökkenő: `x in [2;oo[`.
Függvénytranszformációk:
- `f(x)=x^2` alapfüggvény (parabola)
- `f(x)=(x-2)^2` eltolás az x tengely mentén pozitív irányba 2 egységgel (jobbra)
- `f(x)=-(x-2)^2` tükrözés az x tengelyre
- `f(x)=-(x-2)^2+3` eltolás az y tengely mentén pozitív irányba 3 egységgel (felfelé)
Az alapfüggvényt tehát a (érdemes a csúcspontot, ami alapfüggvény esetén a (0;0) ) eltoltuk a (2;3) pontba és tükröztük (lefelé nyíló parabola lett belőle).
Értelmezési tartomány: `x in RR`
Értékkészlet: `f(x) in RR`, `f(x) in [-oo;3[`
Zérushely: Ahol a függvény értéke nulla.
`-(x-2)^2+3=0` /`color(red)("-3")`
`-(x-2)^2=-3` /`color(red)(*(-1))`
`(x-2)^2=3` /`color(red)("gyökvonás")`
I. `x-2=root()(3)` `rightarrow` `x_1` = `root()(3)+2` `approx` 3,732
II. `x-2=-root()(3)` `rightarrow` `x_2` = `2-root()(3)` `approx` 0,268
A két zérushely a `2+root()(3)` és a `2-root()(3)`.
Szélsőérték: Már megállapítottuk a függvénytranszformációk során; ha lefelé nyíló a parabola, akkor maximuma van, mégpedig a (2;3) pontban.
Monotonitás:
A lefelé nyíló parabolák a szélsőértékig növekednek, utána csökkennek.
Szigorúan monoton növekvő: `x in ]-oo;2]`
Szigorúan monoton csökkenő: `x in [2;oo[`.
2
- Még nem érkezett komment!