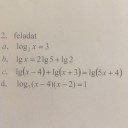Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Sziasztok!
 pohmkati
kérdése
pohmkati
kérdése
446
Legyetek szívesek ezekben a feladatokban segíteni! Kellene a levezetése is! Előre is koszonom!!!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 bongolo
{
bongolo
{  }
megoldása
}
megoldása
Ezt a pár dolgot jegyezd meg:
1) Ha `log_a x = b`, akkor `x = a^b`
2) Szorzat logaritmusa összeg: `log_a (x·y) = log_a x + log_a y`
3) Tört logaritmusa különbség: `log_a (x/y) = log_a x - log_a y`
4) Hatvány logaritmusa szorzat: `log_a (x^b) = b · log_a x`
Ezt a négyet oda-vissza kell tudni. Tipikusan visszafelé kell felismerni...
Persze azt az alap dolgot is kell tudni, hogy `"lg"` azt jelenti, hogy `log_(10)`, valamint hogy `log_a a = 1` (ami egyszerűen az 1) következménye).
a) Ez sima eset, csak az 1) kell hozzá.
b) Itt először a `2· "lg "5`-öt kell nézni, ami olyan, mint a 4) jobb oldala, vagyis
`2· "lg "5 = "lg "2^5 = "lg "32`
Aztán az `"lg "32 + "lg "2`-ről kell rájönni, hogy az meg olyan, mint a 2) jobb oldala, vagyis
`"lg "32 + "lg "2 = "lg " (32·2) = "lg " 64`
Vagyis ez lett:
`"lg "x = "lg "64`
ami azt jelenti, hogy `x=64`
c)
Itt is logaritmusok összege van, ami szorzat logaritmusa, vagyis 2)
`"lg"(x-4)+"lg"(x+3)="lg"(5x+4)`
`"lg"((x-4)(x+3))="lg"(5x+4)`
`(x-4)(x+3)=5x+4`
stb. fejezd be a másodfokút.
Arra kell még figyelni, hogy a másodfokúnak 2 megoldása is lesz, és leet, hogy valamelyik nem jó. Akkor nem jó egy megoldás, ha a logaritmusban lévő érték negatív lenne. Vagyis `x-4 > 0`, `x+3 > 0` és `5x+4 > 0` mind teljesülni kell.
d) Ez is sima eset, csak az 1) kell hozzá, aztén meg kell oldani a másodfokú egyenletet.
1) Ha `log_a x = b`, akkor `x = a^b`
2) Szorzat logaritmusa összeg: `log_a (x·y) = log_a x + log_a y`
3) Tört logaritmusa különbség: `log_a (x/y) = log_a x - log_a y`
4) Hatvány logaritmusa szorzat: `log_a (x^b) = b · log_a x`
Ezt a négyet oda-vissza kell tudni. Tipikusan visszafelé kell felismerni...
Persze azt az alap dolgot is kell tudni, hogy `"lg"` azt jelenti, hogy `log_(10)`, valamint hogy `log_a a = 1` (ami egyszerűen az 1) következménye).
a) Ez sima eset, csak az 1) kell hozzá.
b) Itt először a `2· "lg "5`-öt kell nézni, ami olyan, mint a 4) jobb oldala, vagyis
`2· "lg "5 = "lg "2^5 = "lg "32`
Aztán az `"lg "32 + "lg "2`-ről kell rájönni, hogy az meg olyan, mint a 2) jobb oldala, vagyis
`"lg "32 + "lg "2 = "lg " (32·2) = "lg " 64`
Vagyis ez lett:
`"lg "x = "lg "64`
ami azt jelenti, hogy `x=64`
c)
Itt is logaritmusok összege van, ami szorzat logaritmusa, vagyis 2)
`"lg"(x-4)+"lg"(x+3)="lg"(5x+4)`
`"lg"((x-4)(x+3))="lg"(5x+4)`
`(x-4)(x+3)=5x+4`
stb. fejezd be a másodfokút.
Arra kell még figyelni, hogy a másodfokúnak 2 megoldása is lesz, és leet, hogy valamelyik nem jó. Akkor nem jó egy megoldás, ha a logaritmusban lévő érték negatív lenne. Vagyis `x-4 > 0`, `x+3 > 0` és `5x+4 > 0` mind teljesülni kell.
d) Ez is sima eset, csak az 1) kell hozzá, aztén meg kell oldani a másodfokú egyenletet.
0
- Még nem érkezett komment!