Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matematika 11. osztály Parabola feladat
 sospetra8
kérdése
sospetra8
kérdése
573
1. Adja meg a parabolák jellemző adatait (tengelypont, paraméter, fókusz, vezéregyenes)!
a) y=1/4(x-3)²+1
b) y=-(x+2)²
c) 2x=y²
2. Milyen helyzetű egymáshoz képest az y=1/4x² egyenletű parabola és az x²+(y-1)²=1 egyenletű kör?
Egyetlen egy órán esett szó a paraboláról(beteg voltam), de a nyári feladatsorba, ami az első jegyünket fogja kitenni, 2 feladat is belekerült Köszönöm szépen ha segítetek!
Köszönöm szépen ha segítetek!
a) y=1/4(x-3)²+1
b) y=-(x+2)²
c) 2x=y²
2. Milyen helyzetű egymáshoz képest az y=1/4x² egyenletű parabola és az x²+(y-1)²=1 egyenletű kör?
Egyetlen egy órán esett szó a paraboláról(beteg voltam), de a nyári feladatsorba, ami az első jegyünket fogja kitenni, 2 feladat is belekerült
 Köszönöm szépen ha segítetek!
Köszönöm szépen ha segítetek!
Jelenleg 1 felhasználó nézi ezt a kérdést.
parabola, koordinátageometria, geometria
parabola, koordinátageometria, geometria
1
Középiskola / Matematika
Válaszok
1 Epyxoid
{ Tanár }
megoldása
Epyxoid
{ Tanár }
megoldása
1.
Ha a parabola `(x − u)^2 = 2p*(y − v)` alakú, akkor a paramétere `p`, a tengelypontja `T(u,\ v)`,
a vezéregyenese egyenlete `y = v-p/2` a fókuszpontja pedig `F(u,\ v+p/2)`.
Ha a parabola `(y − v)^2 = 2p*(x − u)` alakú, akkor a paramétere `p`, a tengelypontja `T(u,\ v)`,
a vezéregyenese egyenlete `x = u-p/2` a fókuszpontja pedig `F(u+p/2,\ v)`.
Tehát
a) `y=1/4 (x-3)^2+1 " /"-1`
`1/4 (x-3)^2 = y-1 " /"*4`
`(x-3)^2 = 4(y-1)`
`T(3, 1) ", " p = 2 ", " y_"v" = 0 ", " F(3, 2)`
b) `y=-(x+2)^2 " /"*(-1)`
`(x+2)^2 = -y`
`T(-2, 0) ", " p = -1/2 ", " y_"v" = 1/4 ", " F(-2, -1/4)`
c) `2x=y^2`
`y^2 = 2x`
`T(0, 0) ", " p = 1 ", " x_"v" = -1/2 ", " F(1/2, 0)`
2.
Ha a kör egyenlete `(x-u)^2+(y-v)^2 = r^2` alakú, akkor a középpontja `K(u, v)`, a sugara pedig `r`.
`x^2+(y-1)^2=1`
Tehát a középpontja `K(0, 1)`, a sugara pedig `r=1`, mert `1^2=1`.
`y=1/4 x^2 " /"*4`
`x^2 = 4y`
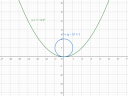
Tehát a tengelypontja `T(0, 0)` az origó és pozitív állású, vagyis egy U-ra hasonlít, mert a paramétere `p=2` pozitív.
Vagyis a parabola az origóból indul, a kör középpontja pedig 1 egységgel felfele tőle 1 egység sugárral, vagyis pont érinti a parabola tengelypontját.
Ha bármi kérdésed lenne nyugodtan írj, szívesen válaszolok!
Ha a parabola `(x − u)^2 = 2p*(y − v)` alakú, akkor a paramétere `p`, a tengelypontja `T(u,\ v)`,
a vezéregyenese egyenlete `y = v-p/2` a fókuszpontja pedig `F(u,\ v+p/2)`.
Ha a parabola `(y − v)^2 = 2p*(x − u)` alakú, akkor a paramétere `p`, a tengelypontja `T(u,\ v)`,
a vezéregyenese egyenlete `x = u-p/2` a fókuszpontja pedig `F(u+p/2,\ v)`.
Tehát
a) `y=1/4 (x-3)^2+1 " /"-1`
`1/4 (x-3)^2 = y-1 " /"*4`
`(x-3)^2 = 4(y-1)`
`T(3, 1) ", " p = 2 ", " y_"v" = 0 ", " F(3, 2)`
b) `y=-(x+2)^2 " /"*(-1)`
`(x+2)^2 = -y`
`T(-2, 0) ", " p = -1/2 ", " y_"v" = 1/4 ", " F(-2, -1/4)`
c) `2x=y^2`
`y^2 = 2x`
`T(0, 0) ", " p = 1 ", " x_"v" = -1/2 ", " F(1/2, 0)`
2.
Ha a kör egyenlete `(x-u)^2+(y-v)^2 = r^2` alakú, akkor a középpontja `K(u, v)`, a sugara pedig `r`.
`x^2+(y-1)^2=1`
Tehát a középpontja `K(0, 1)`, a sugara pedig `r=1`, mert `1^2=1`.
`y=1/4 x^2 " /"*4`
`x^2 = 4y`
Tehát a tengelypontja `T(0, 0)` az origó és pozitív állású, vagyis egy U-ra hasonlít, mert a paramétere `p=2` pozitív.
Vagyis a parabola az origóból indul, a kör középpontja pedig 1 egységgel felfele tőle 1 egység sugárral, vagyis pont érinti a parabola tengelypontját.
Ha bármi kérdésed lenne nyugodtan írj, szívesen válaszolok!

Módosítva: 3 éve
2
-
kazah: A 2. feladatnál érdemes megoldani, mint egyenletrendszert és a helyzetüket a megoldások száma megmondja (nincs közös pont, érinti, metszi). 3 éve 0
-
Ármós Csaba: Igen, érdemes, negyedfokú egyenlet lesz belőle (visszavezethető másodfokúra)!
 3 éve
0
3 éve
0
-
Epyxoid: De csak annyi volt a kérdés, hogy milyen helyzetűek egymáshoz képest... Én nem tartottam érdekesnek azt, hogy van-e metszéspontjuk. 3 éve 1
-
kazah: Igen, csak arra gondoltam, hogy ha nem ilyen egyszerű eset van, amit ránézésre látsz és könnyű számolni vele, akkor oké, de egy nem tengelypontú érintési pontot így nehéz megállapítani. 3 éve 0
-
kazah: nem kell negyedfokúig elmenni, Csabi, az első egyenletben levő `x^2`-et betolod a másodikba és eléggé leegyszerűsödik, két gyök jön ki y-ra, de a -2-es y-ból két nem valós x lesz. A (0;0) is kijön. 3 éve 0
-
Epyxoid: Igen értem, de szerintem nem is érdekes, hogy a tengelypont érinti a kört. Más feladatban ha a helyzetük a kérdés, akkor is kiszámolnám a parabola tengelypontját és állását, a kör középpontját és sugarát és ezek alapján már el lehet képzelni, vagy le lehet rajzolni is a körülbelüli helyzetüket egymáshoz képest. Ha az volna a kérdés, hogy metszik-e egymást az megint más szerintem. 3 éve 1
-
Epyxoid: Igen, kazah jól mondja: a parabola egyenletéből tudjuk, hogy `x^2 = 4y` és ezt is behelyettesíthetjük a kör egyenletébe az `x^2` helyére. 3 éve 0
-
Törölt: Mondjam el hol hibáztál vagy meg találod magadtól? 3 éve -2
-
Epyxoid: Már megint? Pedig 3-szor is átnéztem...
 3 éve
0
3 éve
0
-
Epyxoid: Újra átnéztem. Nekem jónak tűnik
 3 éve
0
3 éve
0
-
bazsa990608: Szép megoldás. Nem hibás csak kötekszik. 3 éve 3
-
Epyxoid: Köszi! Most direkt odafigyeltem azokra a hibákra, amiket legutóbb vétettem, úgyhogy kezdek belejönni!
 3 éve
1
3 éve
1