Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Függvények
 Fruzsiiiiiiiiiiiiiii
kérdése
Fruzsiiiiiiiiiiiiiii
kérdése
377
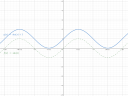
sinx+1
-cos(x+PI/6)-1
ezeket a függvényeket kell jellemeznem és nem értem hogy a monotonitást és a szélső értéket hogyan kell kiszámolni. Valaki elmagyarázná?
-cos(x+PI/6)-1
ezeket a függvényeket kell jellemeznem és nem értem hogy a monotonitást és a szélső értéket hogyan kell kiszámolni. Valaki elmagyarázná?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
3 Epyxoid
{ Tanár }
megoldása
Epyxoid
{ Tanár }
megoldása
Igazándiból ez a feladat nem a számolásról szól... Ha csak nem tanultatok már deriválást, ugyanis a szélsőértékeket és a monotonitást azt a függvény első deriváltjából tudjuk megkapni. Jelen esetben ez a feladat inkább szól a szögfüggvények ismeretéről és a függvénytranszformációról.
1) `sin x+1`
A szinusz függvény értéke 90°-nál 1, 270°-nál pedig -1. Ezek a szélsőértékei. Csakhogy a szinusz függvény periodikus, méghozzá 360° a periódusa, vagyis 90°+360°-nál is 1 a függvény értéke és így tovább. A `sin(x)+1` esetében ez nem változik, ugyanis ez a függvény az eredeti függőlegesen eltoltja 1 egységgel, vagyis a szélsőértékei és a monotonitása is változatlan marad az eredeti szinusz függvényéhez képest. Tehát
Szélsőértékek:
- lokális maximumok: `90°+k*360°, forall k in ZZ` (vagy radiánban: `pi/2+k*2pi, forall k in ZZ`)
- lokális maximumok értéke: `1+1 = 2`
- lokális minimumok: `270°+k*360°, forall k in ZZ` (vagy radiánban: `(3 pi)/2+k*2pi, forall k in ZZ`)
- lokális minimumok értéke: `-1+1 = 0`
Illetve a függvény ezen pontok között nő, vagy csökken. 1-től -1-ig csökken, majd vissza -1-től 1-ig nő. Ez az első periódusban úgy néz ki, hogy 0°-tól 90°-ig nő a fv értéke, majd 90°-től 270°-ig csökken, majd 270°-től ismét nő 360°-ig. Ez három intervallum, de meglehet adni kettővel is, ha az egyiket kicsit eltoljuk, ugyanis 270°-től 360°-ig az ugyanaz, mint -90°-től 0°-ig ha eltoljuk az egészet egy periódussal balra.
Monotonitás:
- (szigorúan) monoton növő: `[-90°+k*360° ", " 90°+k*360°], forall k in ZZ`
(radiánban: `[-pi/2+k*2 pi ", " pi/2+k*2pi], forall k in ZZ`)
- (szigorúan) monoton csökkenő: `[90°+k*360° ", " 270°+k*360°], forall k in ZZ`
(radiánban: `[pi/2+k*2 pi ", " (3 pi)/2+k*2pi], forall k in ZZ`)
2) `-cos(x+pi/6)-1`
Itt már kicsit más a helyzet, de nem sokkal. Ez is el van tolva 1-gyel, csak ez mínusz 1-gyel, de ez nem módosítja a szélsőérték helyeket, se a monotonitást a sima koszinusz függvényhez képest. Viszont a többi igen! Alapból a koszinusz 0°-ban 1, és 180°-ban -1. (Ezek a szélsőértékeink alapból.) De mivel ez a függvény a koszinusz mínusza vagyis `-cos(...)`, ezért az egész függvény megfordul úgy, hogy a minimumokból maximumok lesznek és a maximumokból lesznek a minimumok! Valamint az `x+pi/6` azt csinálja, hogy eltolja a függvényt vízszintesen balra `pi/6`-tal, vagyis `180/6 = 30°`-kal!
Vagyis összegezzük. Alapból 0°-ban lenne 1 a koszinusz, de ez a függvény -1-1=-2 lesz (mivel el van tolva az egész lefele 1-gyel) és nem nullában, hanem -30 foknál! (Ez a balra tolódás következménye.) Illetve eredetileg 180°-nál lenne a koszinusz -1, de itt 1-1=0 lesz (mert -1 mínusza lesz az érték mínusz 1 az eltolás miatt) és nem 180°-nál hanem 180°-30°=120°-nál! Illetve ennek a függvénynek is 360° a periódusa, vagyis ugyanez ismétlődik 360°-onként. Tehát
Szélsőértékek:
- lokális minimumok: `-30°+k*360°, forall k in ZZ` (vagy radiánban: `-pi/6+k*2pi, forall k in ZZ`)
- lokális minimumok értéke: `-(1)-1 = -2`
- lokális maximumok: `120°+k*360°, forall k in ZZ` (vagy radiánban: `(5 pi)/6+k*2pi, forall k in ZZ`)
- lokális maximumok értéke: `-("-1")-1 = 0`
Monotonitás:
- (szigorúan) monoton növő: `[-30°+k*360° ", " 120°+k*360°], forall k in ZZ`
(radiánban: `[-pi/6+k*2 pi ", " (5 pi)/6+k*2pi], forall k in ZZ`)
- (szigorúan) monoton csökkenő: `[120°+k*360° ", " 330°+k*360°], forall k in ZZ`
(radiánban: `[(5 pi)/6+k*2 pi ", " (11 pi)/6+k*2pi], forall k in ZZ`)
1) `sin x+1`
A szinusz függvény értéke 90°-nál 1, 270°-nál pedig -1. Ezek a szélsőértékei. Csakhogy a szinusz függvény periodikus, méghozzá 360° a periódusa, vagyis 90°+360°-nál is 1 a függvény értéke és így tovább. A `sin(x)+1` esetében ez nem változik, ugyanis ez a függvény az eredeti függőlegesen eltoltja 1 egységgel, vagyis a szélsőértékei és a monotonitása is változatlan marad az eredeti szinusz függvényéhez képest. Tehát
Szélsőértékek:
- lokális maximumok: `90°+k*360°, forall k in ZZ` (vagy radiánban: `pi/2+k*2pi, forall k in ZZ`)
- lokális maximumok értéke: `1+1 = 2`
- lokális minimumok: `270°+k*360°, forall k in ZZ` (vagy radiánban: `(3 pi)/2+k*2pi, forall k in ZZ`)
- lokális minimumok értéke: `-1+1 = 0`
Illetve a függvény ezen pontok között nő, vagy csökken. 1-től -1-ig csökken, majd vissza -1-től 1-ig nő. Ez az első periódusban úgy néz ki, hogy 0°-tól 90°-ig nő a fv értéke, majd 90°-től 270°-ig csökken, majd 270°-től ismét nő 360°-ig. Ez három intervallum, de meglehet adni kettővel is, ha az egyiket kicsit eltoljuk, ugyanis 270°-től 360°-ig az ugyanaz, mint -90°-től 0°-ig ha eltoljuk az egészet egy periódussal balra.
Monotonitás:
- (szigorúan) monoton növő: `[-90°+k*360° ", " 90°+k*360°], forall k in ZZ`
(radiánban: `[-pi/2+k*2 pi ", " pi/2+k*2pi], forall k in ZZ`)
- (szigorúan) monoton csökkenő: `[90°+k*360° ", " 270°+k*360°], forall k in ZZ`
(radiánban: `[pi/2+k*2 pi ", " (3 pi)/2+k*2pi], forall k in ZZ`)
2) `-cos(x+pi/6)-1`
Itt már kicsit más a helyzet, de nem sokkal. Ez is el van tolva 1-gyel, csak ez mínusz 1-gyel, de ez nem módosítja a szélsőérték helyeket, se a monotonitást a sima koszinusz függvényhez képest. Viszont a többi igen! Alapból a koszinusz 0°-ban 1, és 180°-ban -1. (Ezek a szélsőértékeink alapból.) De mivel ez a függvény a koszinusz mínusza vagyis `-cos(...)`, ezért az egész függvény megfordul úgy, hogy a minimumokból maximumok lesznek és a maximumokból lesznek a minimumok! Valamint az `x+pi/6` azt csinálja, hogy eltolja a függvényt vízszintesen balra `pi/6`-tal, vagyis `180/6 = 30°`-kal!
Vagyis összegezzük. Alapból 0°-ban lenne 1 a koszinusz, de ez a függvény -1-1=-2 lesz (mivel el van tolva az egész lefele 1-gyel) és nem nullában, hanem -30 foknál! (Ez a balra tolódás következménye.) Illetve eredetileg 180°-nál lenne a koszinusz -1, de itt 1-1=0 lesz (mert -1 mínusza lesz az érték mínusz 1 az eltolás miatt) és nem 180°-nál hanem 180°-30°=120°-nál! Illetve ennek a függvénynek is 360° a periódusa, vagyis ugyanez ismétlődik 360°-onként. Tehát
Szélsőértékek:
- lokális minimumok: `-30°+k*360°, forall k in ZZ` (vagy radiánban: `-pi/6+k*2pi, forall k in ZZ`)
- lokális minimumok értéke: `-(1)-1 = -2`
- lokális maximumok: `120°+k*360°, forall k in ZZ` (vagy radiánban: `(5 pi)/6+k*2pi, forall k in ZZ`)
- lokális maximumok értéke: `-("-1")-1 = 0`
Monotonitás:
- (szigorúan) monoton növő: `[-30°+k*360° ", " 120°+k*360°], forall k in ZZ`
(radiánban: `[-pi/6+k*2 pi ", " (5 pi)/6+k*2pi], forall k in ZZ`)
- (szigorúan) monoton csökkenő: `[120°+k*360° ", " 330°+k*360°], forall k in ZZ`
(radiánban: `[(5 pi)/6+k*2 pi ", " (11 pi)/6+k*2pi], forall k in ZZ`)
Módosítva: 3 éve
0
- Még nem érkezett komment!
 Fruzsiiiiiiiiiiiiiii
válasza
Fruzsiiiiiiiiiiiiiii
válasza
köszönöm szépen a segítséget!
0
-
Epyxoid: Nagyon szívesen! Akartam még képeket is csatolni de elfelejtettem.
 3 éve
0
3 éve
0
-
Fruzsiiiiiiiiiiiiiii: Jajj elnézést, nem tudom hogy kell vissza csinálni ha az a gond hogy megjelöltem az a baj nem igazán értem még hogy hogy működik ez az egész oldal. 3 éve 0
-
Epyxoid: Jaj, nem dehogy. Ezen nem múlik. Mielőtt még beküldeném a választ, azelőtt lehet képeket csatolni hozzá. Utána már sajnos nem. És mivel beküldtem képek nélkül így már nem tudok hozzátenni. De egy másik válaszban még csatolhatok képeket ha szeretnéd!
 3 éve
0
3 éve
0
-
Fruzsiiiiiiiiiiiiiii: rendben, köszönöm szépen : ) 3 éve 1
 Epyxoid
{ Tanár }
válasza
Epyxoid
{ Tanár }
válasza
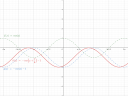
Valahogy így néz ki a két függvény, illetve szaggatottal pár segédfüggvény, amikkel talán könnyebb megérteni hogyan is és mik által tolódik el a függvény az eredeti szögfüggvényekből.
0
-
Fruzsiiiiiiiiiiiiiii: köszönöm szépen 3 éve 0
-
Epyxoid: Nagyon szívesen!
 3 éve
1
3 éve
1