Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Kerlek segits
 timihad350
kérdése
timihad350
kérdése
323
Mit hibaztam?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Általános iskola / Matematika
Válaszok
1 Epyxoid
{ Tanár }
válasza
Epyxoid
{ Tanár }
válasza
a)
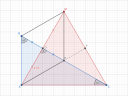
Mivel `AM` és `BC` merőlegesek egymásra, illetve `abs(AD) = abs(DM)`, illetve egyik oldaluk, a `BD` közös és a `D` csúcsnál lévő szögük azonosan derékszög, ezért az `ABD` és az `MBD` háromszögek egybevágóak, vagyis minden szögük és minden oldaluk egyenlő, tehát `AB` és `BM` is!
b)
Az első hiba, hogy `AE` hosszát 8-nak vetted. Nekem így első ránézésre nem egyértelmű, hogy az `E` pont az a `BC` oldalfelezője. De még ha az is (egyébként tényleg az, igazad volt), akkor sem értem, hogy honnan tudjuk, hogy a `BC` hossza mennyi. Induljunk ki abból, amit biztosan tudunk, az pedig a magasság, ami 4 centi. Illetve a szögeket még ügyesen berajzoltad, addig minden tökéletes. Tehát az `ABE` és a `BEM` az két egybevágó egyenlő oldalú háromszög, amiknek a magassága 4. Már ebből is látni, hogy ezeknek az oldala nem 8 lesz, mert az egyenlő oldalú háromszögeknek a magassága az nem az oldalak fele, hanem a `sqrt(3)/2`-ede! De ezt még csak nem is kell tudni. Felírhatjuk mondjuk az `ABD` háromszögben a `hat B` szög szinuszát:
`sin hat B = abs(AD)/abs(AB) => abs(AB) = abs(AD)/sin hat B = 4/(sin 60°) = 8/sqrt 3 ~~ "4,619 cm"`
A másik `AC` oldal hasonló módon kiszámítható. Az `ACD` háromszögben `hat C` szinusza:
`sin hat C = abs(AD)/abs(AC) => abs(AC) = abs(AD)/sin hat C = 4/(sin 30°) = "8 cm"`
Tehát az a különleges helyzet adódott, hogy `abs(AM) = abs(MC) = abs(AC) = "8 cm"`, vagyis az `AMC` egy egyenlő oldalú háromszög! Tehát
`K_(AMC) = 3*8 = "24 cm"`
c)
Mivel `hat A` derékszög és mint megmutattad `ABE` egy egyenlő oldalú háromszög, mivel mindegyik belső szöge egyenlő, így a `hat(CAE)` szög `90°-60° = 30°`, tehát az `ACE` háromszög `A` és `C` csúcsánál lévő szög egyenlő, így a velük szemközti oldalak is egyenlőek, vagyis `abs(AE) = abs(EC)`!
Mivel beláttuk korábban, hogy az `AMC` egy egyenlő oldalú háromszög, illetve hogy a `hat(CAE) = 30°`, ezért az `AE` az a `hat(CAM)` szögfelezője, tehát az egyenlő oldalú háromszög esetében ez egyben ráfekszik a szemközti `CM` oldal oldalfelezőjére, ami egyben a háromszög magassága is, ami merőleges az `MC` oldalra!
Mivel `AM` és `BC` merőlegesek egymásra, illetve `abs(AD) = abs(DM)`, illetve egyik oldaluk, a `BD` közös és a `D` csúcsnál lévő szögük azonosan derékszög, ezért az `ABD` és az `MBD` háromszögek egybevágóak, vagyis minden szögük és minden oldaluk egyenlő, tehát `AB` és `BM` is!
b)
Az első hiba, hogy `AE` hosszát 8-nak vetted. Nekem így első ránézésre nem egyértelmű, hogy az `E` pont az a `BC` oldalfelezője. De még ha az is (egyébként tényleg az, igazad volt), akkor sem értem, hogy honnan tudjuk, hogy a `BC` hossza mennyi. Induljunk ki abból, amit biztosan tudunk, az pedig a magasság, ami 4 centi. Illetve a szögeket még ügyesen berajzoltad, addig minden tökéletes. Tehát az `ABE` és a `BEM` az két egybevágó egyenlő oldalú háromszög, amiknek a magassága 4. Már ebből is látni, hogy ezeknek az oldala nem 8 lesz, mert az egyenlő oldalú háromszögeknek a magassága az nem az oldalak fele, hanem a `sqrt(3)/2`-ede! De ezt még csak nem is kell tudni. Felírhatjuk mondjuk az `ABD` háromszögben a `hat B` szög szinuszát:
`sin hat B = abs(AD)/abs(AB) => abs(AB) = abs(AD)/sin hat B = 4/(sin 60°) = 8/sqrt 3 ~~ "4,619 cm"`
A másik `AC` oldal hasonló módon kiszámítható. Az `ACD` háromszögben `hat C` szinusza:
`sin hat C = abs(AD)/abs(AC) => abs(AC) = abs(AD)/sin hat C = 4/(sin 30°) = "8 cm"`
Tehát az a különleges helyzet adódott, hogy `abs(AM) = abs(MC) = abs(AC) = "8 cm"`, vagyis az `AMC` egy egyenlő oldalú háromszög! Tehát
`K_(AMC) = 3*8 = "24 cm"`
c)
Mivel `hat A` derékszög és mint megmutattad `ABE` egy egyenlő oldalú háromszög, mivel mindegyik belső szöge egyenlő, így a `hat(CAE)` szög `90°-60° = 30°`, tehát az `ACE` háromszög `A` és `C` csúcsánál lévő szög egyenlő, így a velük szemközti oldalak is egyenlőek, vagyis `abs(AE) = abs(EC)`!
Mivel beláttuk korábban, hogy az `AMC` egy egyenlő oldalú háromszög, illetve hogy a `hat(CAE) = 30°`, ezért az `AE` az a `hat(CAM)` szögfelezője, tehát az egyenlő oldalú háromszög esetében ez egyben ráfekszik a szemközti `CM` oldal oldalfelezőjére, ami egyben a háromszög magassága is, ami merőleges az `MC` oldalra!
Módosítva: 3 éve
1
- Még nem érkezett komment!