Első függvény:
Először is tudjuk hogy a Cosx alapfüggvény y = 1 től indulnak a Sin x fügvényhez képest 90°-al eltolva.
Az ábrán láthatod is.
X - π/2 azt jelenti hogy a függvényt 90° al azaz fél randiánnal ami a fél pínek felel meg eltoljuk így kapunk egy Sinx alapfüggvényt amely 0 ról indul π/2-nél 1; míg π nél 0; 1,5π-nél -1 és így tovább.

Tulajdonképpen a Cosx függvényből egy Sinx függényt csinálunk mert pontosan 90°al késik a Sinx függvény a Cosx függvényhez képest de a fél radiános eltolással ezt kompenzáljuk.

Sinx + 1 azt jelenti hogy az alap Sinx függvényt ami 0-ról origóból indul feltoljuk egyel. Más szóval y tengelyen +1 ről fog indulni.

A függvénynek az eltolás miatt

Relatív maximuma x = 180° + 2kπ, k∈Z-ban 2

Relatív minimuma x = 3π/2 + 2kπ, k∈Z-ban 0

Na ebbe beszállok, ez izgalmas lesz

A függvénytranszformációkat ha ismered, akkor menni fog.

1.

- `y=cos x` alapfüggvény

- `y=cos(x-pi/2)` eltolás az x tengely mentén pozitív irányba `pi/2` egységgel. (jobbra)

2.

- `y=sinx` alapfüggvény

- `y=sinx+1` eltolás az y tengely mentén pozitív irányba (felfelé) 1 egységgel

3,

- `y=sinx` alapfüggvény

- `y=sin(x-pi/3)` eltolás az x tengely mentén pozitív irányba `pi/3`-mal (jobbra).

- `y=0.5*sin(x-pi/3)` zsugorítás az y tengely mentén kétszeresére (nyújtás a felére, ahogy tetszik)

- `y=0.5*sin(x-pi/3)+1` eltolás az y tengely mentén pozitív irányba 1 egységgel (felfelé)

Ábrák.

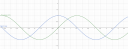
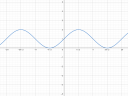
Az első `cos(x-pi/2)` az a koszinusz függvény vízszintesen eltolva `pi/2`-vel. A koszinusz függvénynek alapból -1 és 1 között alakul az értéke, méghozzá úgy, hogy 0-ban 1, `pi/2`-nél (90 foknál) 0, `pi`-nél (180 foknál) -1, `3/2 pi`-nél (270 foknál) ismét nulla, és `2 pi`-nél (360 foknál) ismét 1. Ezen értékek között "hullámzik". Ha ezt eltoljuk jobbra `pi/2`-vel, azaz 90°-kal, akkor egy másik nevezetes függvényt kapunk: a szinuszt! Pont ennyi a különbség a két függvény között, az egyik a másik 90 fokkal eltoltja. 1-es ábra (Persze jó irányba kell eltolni őket, különben lehet, hogy pont egymás negatívjai lesznek.)

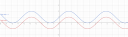
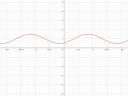
A második függvény `sin x+1` az a szinusz függvény felfelé eltolva 1-gyel. A szinusz függvény olyan, mint az előbb leírt koszinusz függvény, csak az 0-nál 0-ból indul, utána `pi/2`-nél (90 foknál) lesz 1 az értéke, majd `pi`-nél (180 foknál) ismét nulla, aztán `3/2 pi`-nél (270 foknál) -1, és majd `2 pi`-nél ismételten 0. Azzal, hogy ezt eltoljuk +1-gyel, azzal nem -1 és 1 között fog váltakozni a függvény értéke, hanem 0 és 2 között. Pusztán csak ennyi a különbség. 2-es ábra

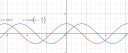
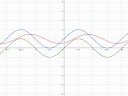
A harmadik függvény esetében pedig már 3 különböző függvénytranszformációt is végeznünk kell az eredeti szinusz függvényen ahhoz, hogy megkapjuk az adott `1+"0,5" sin(x-pi/3)` függvényt: `pi/3`-mal, azaz `180/3 = 60` fokkal el kell tolni jobbra, 1-gyel el kell tolni felfelé, illetve az egész függvényt "függőlegesen össze kell nyomni a felére", vagyis ezúttal nem 0 és 2 között fognak alakulni az értékei, hanem `"0,5"` és `"1,5"` között. 3-as ábra

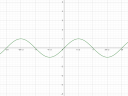
A 4-es ábrán pedig mindegyik függvény egyszerre látszódik. Remélem így már érthetőbb a dolog.

Köszönöm mindenkinek a segítséget nagyon hasznosak voltak : )

Ha az elemzés alatt a jellemzést érted:

1. `f(x)=cos(x-pi/2)`

- Értelmezési tartomány: `x in RR`

- Értékkészlet: `f(x) in RR`, `f(x) in [-1;+1]`

- Folytonosság: folytonos

- Korlátosság: Alulról és felülről is korlátos; K=1; k=-1.

- Monotonitás: `-pi/2+2*k*pi le x le pi/2+2*k*pi` szigorúan monoton növekvő

`pi/2+2*k*pi le x le -3*pi/2+2*k*pi` szigorúan monoton csökkenő

- Zérushely: `x=k*pi`

- Szélsőértékek:

Minimumok: `(-pi/2+2*k*pi;-1)`

Maximumok: `(pi/2+2*k*pi;1)`

Paritás: páratlan

Periodicitás: periodikus, periódusa `2pi`

`k in ZZ`

2. `g(x)=sinx+1`

- Értelmezési tartomány: `x in RR`

- Értékkészlet: `g(x) in RR` ; `g(x) in [0;2]`

- Folytonosság: folytonos

- Korlátosság: Alulról és felülről is korlátos; K=2, k=0

- Monotonitás: `-pi/2+2*k*pi le x le pi/2+2*k*pi` szigorúan monoton növekvő

`pi/2+2*k*pi le x le -3*pi/2+2*k*pi` szigorúan monoton csökkenő

- Zérushely: x = `-pi/2+2*k*pi`

- Szélsőértékek:

Minimum: `(-pi/2+2*k*pi;0)`

Maximum: `(pi/2+2*k*pi;2)`

- Paritás: Se nem páros, se nem páratlan

- Periodicitás: periodikus, periódusa `2pi`.

`k in ZZ`

3. `h(x)=1+0.5sin(x-pi/3)`

- Értelmezési tartomány: `x in RR`

- Értékkészlet: `h(x) in RR`, `h(x) in [0.5;1.5]`

- Folytonosság: folytonos

- Korlátosság: Alulról és felülről is korlátos; K=1,5 ; k=0,5

- Monotonitás: `-pi/6+2*k*pi le x le (5pi)/6+2*k*pi` szigorúan monoton növekvő

`(5pi)/6+2*k*pi le x le (11pi)/6+2*k*pi` szigorúan monoton csökkenő

- Zérushely: Nincs

- Szélsőértékek:

Minimum: `(-pi/6+2*k*pi;0.5)`

Maximum: `((5pi)/6+2*k*pi;1.5)`

- Paritás: Se nem páros, se nem páratlan

- Periodicitás: periodikus, periódusa `2pi`.

`k in ZZ`