Legyen `x` a csúcs eltolásának mértéke, és `d` a csúcs (`P`) távolsága az alapkör középpontjától, `K`-tól. Az alap sugara pedig `r`!
`r = "12 cm" ``", "`` x = "5 cm" ``", "`` d = "17 cm"`

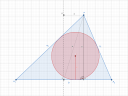
Mivel alapból az egyeneskúp tengelyesen szimmetrikus, így az alapjára merőleges, a csúcsot tartalmazó keresztmetszetek közül nincs kitüntetett, mivel minden irányból ugyanúgy néz ki. Viszont ebben az esetben, mivel a kúp csúcsát eltoltuk, ezért van a testnek egy, a többinél "érdekesebb" keresztmetszete, ami merőleges az alapra, tartalmazza a csúcsot és az alap középpontját is! Jelen esetben elég ezt az egyetlen keresztmetszetet vizsgálnunk olyankor, amikor az egyeneskúpoknál használt képletek nem működnek. Az ábrámon is ez a keresztmetszet látható!

Először is számoljuk ki a test magasságát, mert azt cselesen két másik adattal adták meg. A csúcs távolsága `d` és eltolása `x` egy derékszögű háromszöget alkot a keresett magassággal, ami legyen `h`. Tehát:
`d^2 = h^2+x^2 => h = sqrt(d^2-x^2) = sqrt(17^2-5^2) = sqrt 264 = 2 sqrt 66 ~~ "16,248 cm"`

Ezek után közvetlenül adódik a térfogat, mivel minden gúlaszerű testre igaz, hogy a térfogata egyenlő az alapterülete és a magasságának szorzatának harmadával!
`V_"ferde kúp" = (T_"alap"*h)/3 = (pi r^2*h)/3 = (12^2 pi*2 sqrt 66)/3 = 96 pi sqrt(66) ~~ "2 450,152 cm"^3`

A felszínnel viszont már nem járunk ilyen jól... Egy közönséges kúp felszínéhez kellene az alkotó, ami a távolsága a csúcsnak az alap kerületétől, ami egy adott hossz lenne. Jelen esetben viszont nincs egy adott értéke, az függ attól, hogy milyen szögben nézzük a testet, így a palást nem egy szabályos körcikk ha kiterítjük a síkra, hanem egy torzított. Tehát a felszín kiszámolása túl bonyolult lenne. Persze nem lehetetlen, de én inkább kihagynám, mivel semmi tanulságos nem volna benne.

A beírható gömb sugarához, ami legyen `rho`, pedig azt a kitűntetett keresztmetszetet érdemes megvizsgálni, amit korábban említettem, mert azon van rajta az összes olyan pont, ami érdekes a beírható gömb szempontjából, így az ebbe a keresztmetszetbe elférő kör sugara meg fog egyezni a keresett gömb sugarával! Ez a keresztmetszet egy háromszöget ad, aminek minden oldala különbözik, így ez egy teljesen általános háromszög. Viszont ismerjük a leghosszabb oldalát, mert az az alap átmérője `"24 cm"`, illetve a magasságát, ami maga a test magassága is, `h`. Ez a magasság 2 derékszögű háromszögre osztja a keresztmetszetet, amiknek közös az egyik befogójuk: a magasság `h`, a másik oldaluk pedig számolható, ugyanis az egyik annyival rövidebb az alap sugaránál, amennyivel eltoltuk a kúp csúcsát, a másik pedig annyival hosszabb! Tehát az átfogók
`a_1^2 = h^2+(r-x)^2 => a_1 = sqrt(264+7^2) = sqrt 313 ~~ "17,692 cm"`
`a_2^2 = h^2+(r+x)^2 => a_2 = sqrt(264+17^2) = sqrt 553 ~~ "23,516 cm"`

Tehát a beírható kör/gömb sugara:
`rho = (2T)/K = (2*(2r*h)/2)/(2r+a_1+a_2) = (2*12*2 sqrt 66)/(2*12+sqrt 313+sqrt 553) ~~ "5,980 cm"`

`V_rho = (4 pi rho^3)/3 ~~ "895,840 cm"^3`