Másodfokú függvények jellemzése.

Példák:

`f(x)=x^2+8x+11`

`g(x)=-x^2+6x+12`

`h(x)=2x^2-4x-1`

Értelmezési tartomány, értékkészlet, szélsőérték, zérushely, monotonitás, paritás, periodicitás, folytonosság, korlátosság; általában ezeket a jellemzőket kell leírni. Ha csak azt a párat, akkor csak azokat gyakorold.

Példa megoldva:

`i(x)=3x^2-12x+18`

`3x^2-12x+18` = `3*(x^2-4x)+18` = `3*(x-2)^2-(3*4)+18` = `3(x-2)^2+6`

A négyzetes tag előjeléből megtudod, ha pozitív, akkor felfelé nyíló parabola lesz; ha negatív, akkor lefelé nyíló parabola.

Az értelmezési tartomány ezeknél általában mindig a valós számok halmaza; az értékkészlet pedig, mivel felfelé nyílik a parabola, valamilyen számnál nagyobb-egyenlő. A kapott átalakítás után a zárójelben levő kifejezés sokat segít, a zárójeles kifejezés ha nullával egyenlő, akkor megtudjuk, hogy a függvényérték 6 vagy annál nagyobb lehet csak.

Értékkészlet: `x in RR`, `x in [6;oo[`.

Ha felfelé nyílik a parabola, akkor minimuma van; a minimum helye az x=2-nél lesz; értéke pedig (már kiszámoltuk) 6. Minimum: (2;6).

Monotonitás: Amíg el nem éri a szélsőértéket, addig csökkenő, utána növekvő; ha lefelé nyíló parabola van, akkor fordítva:

`]-oo;6]` szigorúan monoton növekvő

`[6;oo[` szigorúan monoton csökkenő.

Korlátosság: A felfelé nyíló parabola alulról korlátos, a korlát pedig mindig az az érték, amit az alsó korlátnál felvesz. Lefelé nyílónál fordítva.

K: 6.

Periodicitás: Nem periodikus, szögfüggvényeknél jellemző.

Paritás: Ha az origóra tudod tükrözni, akkor páratlan; ha az y tengelyre, akkor páros. Ez egyik sem, szóval se nem páros, se nem páratlan. A másodfokú függvények ha van paritás, akkor csak a páros jöhet szóba, a hiányos `ax^2+c` formájúak párosak.

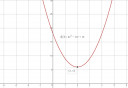
Ha ábrázolni kell, akkor részletesen le kell írni a függvénytranszformációkat:

`y=3(x-2)^2+6`

I. `y=x^2` alapfüggvény

II. `y=(x-2)^2` eltolás az x tengely mentén pozitív irányba 2 egységgel.

III. `y=3(x-2)^2` nyújtás az y tengely mentén háromszorosára. (ha 1-nél kisebb, akkor zsugorítás; ha mínusz előjel van, akkor tükrözés az x tengelyre)

IV. `y=3(x-2)^2+6` eltolás az y tengely mentén pozitív irányba 6 egységgel.

Zérushely: ahol metszi az x tengelyt. A kifejezést nullával tesszük egyenlővé és megoldjuk.

`3(x-2)^2+6=0`

`3(x-2)^2=-6`

Az egyenletnek nincs megoldása, a függvénynek nincs zérushelye.

Tengelymetszet: ahol az y tengelyt metszi a függvény, x helyére 0-t helyettesítünk be és megoldjuk:

`y=3*(0-2)^2+6` = `3*2^2+6` = `3*4+6` = `12+6` = 18

Az y tengelyt a (0;18) pontban metszi.

Ami nem kell, akkor azokat szelektáld. Ha csak a minimumot kell megállapítani, akkor csak azt nézd.