`h = "15 cm" ``", "`` f = "10 cm"`

Ábrák a másik válaszom alatt!

Itt megint csak egy vázlattal kezdeni sokat segít, mert rögtön kiszúrhatjuk, hogy egy szabályos hatszög hosszabbik átlója áthalad a hatszög középpontján, ami nagyon fontos, ugyanis ha ezeket az átlókat mind behúzzuk, amik mind áthaladnak a középponton, akkor 6 darab egyenlő oldalú háromszöget kapunk, amiknek az oldala az átló fele, vagyis a hatszög oldala is az átló fele. Tehát egyből megvan a hatszög oldalának hossza.
`a = f/2 = "5 cm"`

Először is nézzük ennek a térfogatát.
`V_"gúla" = (T_"alap"*h)/3`

Az alap terület pedig 6 darab egyenlő oldalú háromszögből áll, vagyis
`T_"alap" = 6*T_("alap" /_\\)`

Egy egyenlő oldalú háromszög területe, mint mindegyik háromszögé:
`T_("alap" /_\\) = (a*m_a)/2`

Egy egyenlő oldalú háromszög magassága pedig könnyen megkapható a Pitagorasszal, ha szokásos módon a magasság mentén megfelezzük a háromszöget. Ekkor
`a^2 = (a/2)^2+m_a^2 => m_a = sqrt(a^2-a^2/4) = sqrt 3/2*a`

Vagyis
`T_("alap" /_\\) = (a*(sqrt 3/2*a))/2 = sqrt 3/4*a^2`

`T_"alap" = cancel 6_3*(sqrt 3/cancel 4_2*a^2) = (3 sqrt 3)/2*a^2`

`V_"gúla" = (((3 sqrt 3)/2*a^2)*h)/3 = sqrt 3/2*a^2*h ~~ "324,760 cm"^3`

Na most. Oka volt, hogy levezettem ezt a képletet. Ennek a gúlának levágjuk a csúcsát. Én úgy értelmezem, hogy a csonka gúla magassága lesz az eredeti `75%`-a, tehát a csúcs magassága az eredeti `25%`-a. Ez azért fontos, mert a levágott csúcs az középpontosan hasonló az eredeti gúlához. Azaz mindenben ugyanolyan, mint az eredeti gúla, csak negyed akkor. (Ez könnyen belátható. Ha nem világos miért, akkor ezt is elmagyarázhatom.) Negyed akkora az oldala és negyedakkora a magassága, márpedig csak ez határozza meg a térfogatát. Vagyis ennek a kisebb gúlának a térfogata arányos az eredeti gúláéval, és az arány a kettő között `"0,25"^3`! Mutatom miért.

A levágott gúla oldala az eredeti negyede, vagyis `a*"0,25"`, ahogy a magassága is, vagyis a magassága `h*"0,25"`, vagyis a térfogata:
`V_"csúcs" = sqrt 3/2*("0,25"a)^2*("0,25"h) ``=`` sqrt 3/2*"0,25"^2 a^2*"0,25" h ``=`` sqrt 3/2*a^2*h*"0,25"^3 ``=`` V_"gúla"*"0,25"^3`

Tehát végül:
`V_"csonka gúla" = V_"gúla"-V_"csúcs" = V_"gúla"-V_"gúla"*"0,25"^3 = V_"gúla"(1-"0,25"^3) = 63/64*V_"gúla" ~~ "319,685 cm"^3`

A felszín esetében már nem ilyen egyszerű a helyzet, de attól se kell annyira megijedni. Az alaplap területe megvan. A fedőlap pedig egy negyed akkora oldalú szabályos hatszög, vagyis a területe az alaplapéhoz képest a `"0,25"^2`. Ez hasonlóan látható be, mint ahogyan a térfogatnál csináltuk, de ha csak simán kiszámolod a negyed oldal hosszal a területet az is ugyanazt fogja adni, ha neked úgy egyszerűbb és érthetőbb.

Az egyedüli nehézséget a palást okozza, ami 6 darab húrtrapézból áll, amik az oldallapok. Ezeket kiszámolhatjuk a trapéz terület képletével, amihez csak a magasság hiányzik. Vagy kiszámolhatjuk az eredeti gúla háromszög oldallapjából kivonva a levágott gúla oldallapját, ami ugyanúgy háromszög, viszont itt is a magasságok hiányoznak, tehát mindegy melyiket választjuk, kell az oldallapok magassága. Én a trapéz képletét fogom használni:
`P = 6*((a+c)/2*m_"o csonka")`, ahol `c` a trapéz másik alapja, ami jelen esetben a levágott csúcs alapjának oldala, ami az eredeti negyede, vagyis `c = a*"0,25"`

A keresett magasságot úgy tudjuk megkapni, hogy az eredeti gúla keresztmetszetét nézve, a magasság mentén kapunk egy derékszögű háromszöget, aminek az oldalai a gúla magassága `h`, az alap egyik egyenlő oldalú háromszögének a magassága `m_a`, és az oldallap magassága, mondjuk legyen `m_o`. Ekkor
`m_o^2 = h^2+m_a^2 => m_o = sqrt(h^2+(sqrt 3/2*a)^2) = sqrt(h^2+3/4 a^2) = (5 sqrt 39)/2 ~~ "15,612 cm"`

A levágott kisebb gúla oldallapjának a magassága az megint csak az eredeti negyede, vagyis a csonka gúla oldallapjának a magassága
`m_"o csonka" = m_o-m_o*"0,25" = m_o(1-"0,25") = 3/4*m_o = (15 sqrt 39)/8 ~~ "11,709 cm"`

Ezzel megvan minden adat a felszínhez!
`F_"csonka gúla" = T_"alap" + T_"fedőlap" + P = T_"alap" + T_"alap"*"0,25"^2 + P = 17/16*T_"alap" + P`

`T_"alap" = (3 sqrt 3)/2*5^2 = (75 sqrt 3)/2 ~~ "67,952 cm"^2`

`P = 6*((5+5*"0,25")/2*(15 sqrt 39)/8) = 6*25/8*(15 sqrt 39)/8 = (1125 sqrt 39)/32 ~~ "219,551 cm"^2`

`F_"csonka gúla" = 17/16*(75 sqrt 3)/2 + (1125 sqrt 39)/32 ``=`` (1275 sqrt 3)/32 + (1125 sqrt 39)/32 ~~ "288,562 cm"^2`

Ábrák a másik válaszom alatt!

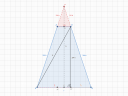
A keletkezett csonka gúlának több testátlója is van, szám szerint `(6*3)/2 = 9`, de hossz szerint, csak két különböző van, mint ahogyan az alaplapnak, a szabályos hatszögnek is csak kétféle hosszú átlója van. A testátlók is ezekkel vannak párban. Mivel a kérdés úgy fogalmaz, hogy "A testátlót", ezért én a feladatban megadott, hosszabb átlóhoz tartozó, leghosszabb testátlót számolom csak ki. Így is rengeteget kell vesződni ezzel a feladattal. Érettségin biztos nem lesz ilyen, csak szólok. Mármint hasonló biztos lesz, de ennél azért egyszerűbb lesz. Ez már túl melós ahhoz, hogy érettségin legyen.

Na de lássuk a testátlót. Csináltam hozzá ábrát, mert különben elég nehéz volna elképzelni, hogy mi történik (persze nem lehetetlen, csak egy jó kép kell hozzá a fejben). Ha a feladatban megadott átló mentén kettészeljük a csonka gúlát, akkor megint csak egy húrtrapézt kapunk. Ennek a trapéznak a nagyobbik alapja az az `f`, a másik alapja az a fedőlap ugyanezen átlója, ami, mint tudjuk negyed akkora, mint az eredeti, mert a levágott gúlának mindene negyed akkora, a trapéz szárai pedig a csonka gúla oldaléle - ez eredeti gúla oldalélét `b`-vel jelölöm, de végül nem kellett kiszámolnom. Nekünk ennek a trapéznak az átlója kell, mert az a csonka gúla legnagyobb testátlója. Ezt úgy kaphatjuk meg, hogy behúzzuk a magasságot a `D'` csúcsba, ami a testátlóval - én `q`-nak nevezem - egy derékszögű háromszöget alkot. Viszont ennek nem ismerjük a harmadik oldalát, az `f_2`-t. Ezt úgy kaphatjuk meg, ha megvizsgáljuk az `f` másik szakaszát, az `f_1`-et. Az `f_1` a berajzolt magassággal egy másik derékszögű háromszöget alkot a csonka gúla oldalélével. Ez a háromszög a `D'D''D` hasonlít a `PKD` háromszögre. Lényegében ugyanaz a háromszög, csak az oldalai 3/4 olyan hosszúak, így az `f_1` is a háromnegyede a `PKD` megfelelő oldalának, ami jelen esetben `f/2`. Vagyis
`f_1 = 3/4*f/2 = 3/4*10/2 = 15/4 = "3,75 cm"`

Az `f_2` tehát
`f_2 = f-f_1 = 10-15/4 = 25/4 = "6,25 cm" `

Vagyis a keresett testátló:
`q^2 = (3/4 h)^2 + f_2^2 => q = sqrt(9/16*15^2+25^2/16) = (5 sqrt 106)/4 ~~ "12,870 cm"`

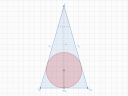
Na ez is megvan. A beírt gömb sugarának megállapításához pedig elég megint csak egy keresztmetszetet néznünk. Természetesen nem arra a keresztmetszetre van szükség, mint amelyik a testátlóhoz kellett. Jó szemét ez a feladat, de nem baj, annyira nem nehéz a számolás, csak a rengeteg alakzat között kell kiigazodni és meglátni mi mennyi és hogyan néz ki... A beírható gömb maximum háromféle dologgal tud érintkezni a csonka kúpban legjobb esetben is, de általában csak kettővel érintkezik: az egyik az alaplap, azzal mindenképp érintkezik, a másik pedig vagy a fedőlap, hogy ha nem elég magas a test ahhoz, hogy az oldallapokkal érintkezzen a gömb. Ha pedig elég magas a test, akkor az oldallapok fogják megszabni, hogy mekkora is lehet ez a gömb, ekkor viszont a fedőlappal nem érintkezik. Jelen esetben az utóbbi a helyzet. Láthatjuk az adatokból is, hogy az eredeti gúla magassága nagyobb még az alap hatszög átlójánál is, úgyhogy ez egy nagyon magas, keskeny gúla. Tehát azt már tudjuk, hogy a gömb az oldallapokkal fog majd érintkezni, az ábrán látszik is majd, hogy a magasság bőven elég nagy ahhoz, hogy ne azon múljon a gömb mérete.

Ezek után azt kell meglátnunk, hogy az oldallapokat vajon hol fogja érinteni a gömb? Szerintem egyszerű elképzelni, de nem magamból kell most kiindulni. Mivel a gúla/csonka gúla sarkos, hiszen hatszög az alapja, ezért belülről egy gömb nem fog tudni érintkezni a test éleivel és csúcsaival, mert azok "kitüremkednek". Egy sima gömbfelszín előbb találkozik az oldallapokkal minthogy elérjen az élekig és az oldallapokat is pont félúton, a húrtrapéz szimmetriatengelynénél fogja érinteni, ezért ebben a vonalban célszerű venni a keresztmetszetet. Az egyik ábrán bejelölöm majd, hogy a két keresztmetszet között mi a különbség.

Mivel pusztán az adatok arányából kizártuk azt a lehetőséget, hogy a csonka gúla magassága határozza meg a beírt gömb méretét, ezért nézhetjük az eredeti gúla keresztmetszetét, mert abba is ugyanakkora gömb fér el, mint a csonka gúlába. Tehát a gúla oldallap felezője mentén vett keresztmetszetből egy egyenlő szárú háromszöget kapunk. Ennek a háromszögnek az alapja a gúla alaplapján lévő egyenlő oldalú háromszögek magasságának a kétszerese (`2*m_a`). A szára pedig az oldallapok magassága, vagyis az `m_o`. Ebbe a háromszögbe beírható kör sugara megegyezik a csonka gúlába írható gömb sugarával, ugyanis ezen keresztmetszet mentén érintkezik a gömb a csonka gúlán belül, vagyis ez a legnagyobb keresztmetszet, ami közvetlenül meghatározza annak sugarát.

Ennek a háromszögnek a beírt kör sugarát ugyanúgy kapjuk, mint bármelyik másik háromszögét:
`r = (2T)/K`

Vagyis szükségünk van ennek a háromszögnek a területére és a kerületére és meg is vagyunk! Mivel ismerjük a háromszög alapját és a magasságát is, ezért a területe egyből adódik:
`T = (cancel 2*m_a*h)/cancel 2 = m_a*h = (5 sqrt 3)/2*15 = (75 sqrt 3)/2 ~~ "64,952 cm"^2`

Illetve a kerület is adott, ahhoz is tudunk mindent, hála a jó égnek:
`K = 2*m_a+2*m_o = cancel 2*(5 sqrt 3)/cancel 2 + cancel 2*(5 sqrt 39)/cancel 2 = 5(sqrt 3+sqrt 39) ~~ "39,885 cm"`

Vagyis a beírható kör/gömb sugara:
`r = (2*(75 sqrt 3)/2)/(5(sqrt 3+sqrt 39)) ``=`` (cancel 75_15 sqrt 3)/(cancel 5(sqrt 3+sqrt 39)) ``=`` (15 sqrt 3)/(sqrt 3+sqrt 39) ``=`` 15/(1+sqrt 13) ~~ "3,257 cm"`

`V_"gömb" = (4 pi r^3)/3 ~~ "144,716 cm"^3`

`F_"gömb" = 4 pi r^2 ~~ "133,300 cm"^2`