Csatoltam képet.

Az ilyen feladatoknál nagyon fontos a rajz, hogy lássuk, hogy pontosan hogyan is helyezkedik el az, ami a feladatban meg van határozva. Hogy lássuk, hogy pontosan mit is tudunk, illetve hogy könnyebben tudjunk következtetéseket levonni az elrendezésből...

Miután csináltunk egy vázlatot után érdemes minél több helyen berajzolni a sugarat, minden említésre méltó pontnál, mert minél több helyen szerepel, annál többet segít. Pl itt is az volt az első gondolatom, hogy akárhogyan is metszi a húr a nagyobbik kört, akkor is ahol metszi oda behúzható a sugár, amivel máris alkottunk egy háromszöget. Ez volna ugyanis a cél, mert egy háromszögről rengeteg mindent meg tudunk határozni relatíve kevés adatból...

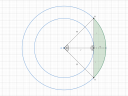
Egy lehetséges háromszög például az `MNO` háromszög (a csatolt ábrán), amit a feladatban leírt húr és a nagykörnek két sugara alkot, így tehát egyenlő szárú. Mivel a harmadik oldalhoz, a húrhoz (`2r`) tartozó magasság (`r`) hossza az oldal fele, ezért a szárak közötti szög derékszög, de ez nem annyira egyértelmű, úgyhogy inkább felezzük meg a magasság mentén. Ekkor már biztosan derékszögű háromszöget kapunk, ugyanis az érintési pontba húzott sugár mindig merőleges az érintő egyenesre. Ez a háromszög (`OME`) is egyenlő szárú, az oldalai pedig csakis a két sugárból állnak: a két befogó a kiskör sugara, az átfogó pedig a nagykör sugara.
`R^2 = r^2+r^2`
`R^2 = 2r^2 " /" sqrt`
`R = sqrt 2 r`

Tehát ahhoz, hogy a feladatban meghatározott elrendezést kapjuk, ahhoz a nagyobb kör sugarának a kisebb `sqrt 2`-szöröse kell hogy legyen. Így aztán végtelen sok ilyen elrendezés létezik. Nekünk egy olyan kell, amiben a két sugár különbsége pont 9!
`{(R = sqrt 2 r), (R = r+9):}`

`sqrt 2 r = r+9 " /"-r`
`sqrt 2 r-r = 9`
`r(sqrt 2-1) = 9 " /":(sqrt 2-1)`
`r = 9/(sqrt 2-1) = 9(sqrt 2+1) ~~ "21,728 cm"`
`R = 9(sqrt 2+2) ~~ "30,728 cm"`

A kerületek:
`K_r = 2 pi r = 18 pi (sqrt 2+1) ~~ "136,521 cm"`
`K_R = 2 pi R = 18 pi (sqrt 2+2) ~~ "193,069 cm"`

Egy körszelet területét pedig úgy kapjuk, hogy ha a hozzátartozó körcikk területéből kivonjuk a benne lévő háromszöget, jelen esetben az `OMN` háromszöget. Mivel tudjuk, hogy ez a háromszög két egyenlő szárú derékszögű háromszögre osztható, és mivel maga a háromszög is egyenlő szárú, ezért ez a háromszög is derékszögű. És mivel derékszögű, ezért a hozzá tartozó körcikk pont egy negyedkör! Tehát
`(R^2 = [9(sqrt 2+2)]^2 = 81(2+4 sqrt 2+4) = 81(6+4 sqrt 2) = 2*81(3+2 sqrt 2))`
`T_"körszelet" = (R^2 pi)/4-(R*R)/2 ``=`` (R^2 pi)/4-(2R^2)/4 ``=`` (R^2 (pi-2))/4 = (cancel 2*81(3+2 sqrt 2)(pi-2))/cancel 4_2 ``=`` 81/2 (3+2 sqrt 2)(pi-2) ~~ "269,474 cm"^2`