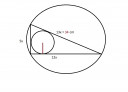
Egy derékszögű háromszög köré írt körének sugara az átfogó fele lesz, ha még emlékszel a Thalész-tételre.

Az átfogó hossza:

c = `root()((5x)^2+(12x)^2)` = `root()(25x^2+144x^2)` = `root()(169x^2)` = 13x cm

13x = 34 cm `rightarrow` x = `34/13` cm

A beírt sugárra van képlet, amit a függvénytáblázatban megtalálsz:

r= `2*T/K` = `(a*b)/(a+b+c)`

T = `(a*b)/2` = `(5x*12x)/2` = `30x^2`

K = `5x+12x+13x` = 30x

r = `2*(30x^2)/(30x)` = 2x = `2*34/13` = `68/13` cm `approx` 5,23 cm

`R=17` `cm`
`a=5x`
`b=12x`
`c=sqrt(25x²+144x²)=sqrt(169x²)=13x`

`R=c/2`
`R=(13x)/2`

`(13x)/2=17` `//*2`
`13x=34` `//÷13`
`x=(34)/(13)`

`a=5*(34)/(13)=(170)/(13)` `cm`
`b=12*(34)/(13)=(408)/(13)` `cm`
`c=13*(34)/(13)=34` `cm`

`s=(a+b+c)/2`
`s=((170)/(13)+(408)/(13)+34)/2=(510)/(13)` `cm`

`T=sqrt(s(s-a)(s-b)(s-c))`
`T=sqrt((510)/(13)(((510)/(13)-(170)/(13))((510)/(13)-(408)/(13))((510)/(13)-34))`
`T=(34680)/(169)` `cm²`

`T=sr`
`(34680)/(169)=(510)/(13)*r` `//÷(510)/(13)`
`r=(68)/(13)≈5,23` `cm`

Remélem, nem néztem el sehol.

Nem kell amúgy semmilyen tételt sem tudni. Ha van függvénytáblázat nálad akkor benne van, hogy
`T = (abc)/(4R)`

Illetve tudjuk, hogy a derékszögű háromszög területe elég szerencsésen adódik, mivel a két befogója merőleges egymásra, így egymás magasságai, és minden háromszögre igaz, hogy az oldal és a hozzá tartozó magasság szorzatának fele a terület, így
`T = (ab)/2`

Tehát
`cancel(ab)/cancel 2 = (cancel(ab)c)/(cancel(4)_2R) " /"*2R`
`2R = c`

Ezzel megvan a hiányzó összefüggésünk a feladat megoldásához! Persze végső soron könnyebb megjegyezni, hogy derékszögű háromszögnél ez a helyzet, mint levezetni.